Probleme cu secvente

(Categoria Diverse, autor Cosmin Negruseri)

• Cuprins
• Introducere
• Problema 1 ( Subsecventa de suma maxima )

Introducere

Acest articol prezinta o serie de probleme inrudite cu problema subsecventei de suma maxima, insotite de rezolvari eficiente. Problemele prezentate pot aparea oricand ca subprobleme in concursurile de programare, studierea lor marind in mod util bagajul de cunostinte al unui elev pasionat de algoritmica.

Problema 1 ( Subsecventa de suma maxima )

Se da un şir A = ( a₁, a₂, ... , a_N) de numere intregi. Sa se determine o subsecventa ( a_i, a_i+1, ... , a_j) care sa aiba suma maxima.

Exemplu

Pentru secventa de numere (-1, 2, 3, -4, -2, 2, 1, -3, -2, -3, -4, 9, -2, 1, 7, 8, -19, -7, 2, 4, 3), o subsecventa de suma maxima este (9, -2, 1, 7, 8).

Rezolvare

Prima rezolvare care ne vine in minte este: pentru orice subsecventa sa ii determinam suma, iar apoi sa determinam maximul acestor sume. Aceasta solutie are complexitatea O(N^3).

bestSum = -infinit;
for (i = 1; i <= N; i++) {
   for (j = i; j <= N; j++) {
         sum = 0;
         for (k = i; k <= j; k++) sum += a[ k ];
         if (bestSum < sum) bestSum = sum;         
   }
}

Este evident ca se calculeaza anumite sume partiale de mai multe ori. Pentru a reduce complexitatea la O(N²) este necesar sa observam ca suma subsecventei a[ i..j ] este egala cu suma subsecventei a[ i..j-1 ], la care se aduna a[ j ].
Alta idee este de a pastra intr-un sir sum[ i ] - suma elementelor din subsecventa a[ 1..i ]. Pentru a determina suma elementelor din subsecventa a[ i..j ] putem face calculul sum[ i ] - sum[ j-1 ] (complexitate O(N²)).

sum[ 0 ] = 0;
for (i = 1; i <= N; i++) sum[ i ] = a[ i ] + sum[ i - 1 ];
bestSum = -infinit;
for (i = 1; i <= N; i++) {
   for (j = i; j <= N; j++) {
         if (bestSum < sum[ i ] – sum[ j - 1 ]) bestSum = sum[ i ] - sum[ j - 1 ];
   }
}

Putem sa rafinam aceasta idee calculand pentru fiecare indice i numarul best[ i ] ( subsecventa de suma maxima ce are capatul drept in i ). Este usor de observat ca best[ i ] = max( sum[ i ] - sum[ j-1 ] ), unde j ia valori de la 1 la i. Relatia anterioara este echivalenta cu best[ i ] = sum[ i ] – min( sum[ j-1 ] ). Obtinem astfel un algoritm liniar care ne determina subsecventa de suma maxima.

sum[ 0 ] = 0;
for (i = 1; i <= N; i++) sum[ i ] = a[ i ] + sum[ i-1 ];
min = sum[ 0 ];
bestSum = -infinit;
for (i = 1; i <= N; i++) {
     best[ i ] = sum[ i ] - min;
     if (min > sum[ i ]) min = sum[ i ];
     if (bestSum < best[ i ]) bestSum = best[ i ];
}

Putem incerca o abordare bazata pe paradigma divide et impera. La fiecare pas impartim sirul in jumatate si aflam subsecventele de suma maxima din cele doua jumatati. Dupa aceea trebuie sa gasim subsecventa de suma maxima care are cate un capat in fiecare din cele doua jumatati ale sirului. Gasim aceasta secventa prin alipirea sufixului de suma maxima a primei jumatati cu prefixul de suma maxima a celei de-a doua.

int getMaxSubsequence(int l, int r) {
     if (l == r) return a[ l ];
     mid = (l + r) / 2;
     bestL = getMaxSubsequence(l, mid);
     bestR = getMaxSubsequence(mid + 1, r);
     suf = 0; 
     pre = 0; 
     maxSuf = -infinity; 
     maxPre = -infinity;
     for (i = mid; i >= l; i--) {
           suf += a[ i ];
           if (maxSuf < suf) maxSuf = suf;
     }
     for (i = mid + 1; i <= r; i++) {
           pre += a[ i ];
           if (maxPre < pre) maxPre = pre;    
     }
     return max(bestL, max( bestR, maxPre + maxSuf ));
}

O idee bazata pe paradigma programarii dinamice ar fi sa folosim un sir best[ i ], reprezentand suma maxima a unei subsecvente ce se termina in a[ i ]. Se poate demonstra prin inductie ca sirul best satisface urmatoarea recurenta best[ i ] = max( a[ i ], best[ i-1 ] + a[ i ] ).

bestSum = a[ 1 ];
for (i = 1; i <= N; i++) {
     best[ i ] = a[ i ];
     if (best[ i ] < best[ i-1 ] + a[ i ]) best[ i ] = best[ i-1 ] + a[ i ];
     if (bestSum < best[ i ]) bestSum = best[ i ];
}

Alta idee ar fi sa partitionam sirul in subsecvente, astfel incat fiecare dintre acestea sa aiba ambele capete cat mai mici posibile si suma elementelor subsecventei sa fie negativa. Pe exemplul data avem [-1], [2, 3, -4, -2], [2, 1, -3, -2], [-3], [-4], [9, -2, 1, 7, 8, -19, -7], [2, 4, 3]. Este evident ca o subsecventa de suma maxima va avea primul capat la inceputul unei astfel de subsecvente. Acest lucru se explica prin faptul ca in caz contrar secventa poate fi marita in stanga ( orice secventa din cele alese pentru partitionare are toate prefixele de suma pozitiva, in afara de prefixul ce reprezinta intreaga subsecventa ). De asemenea, orice subsecventa de suma maxima nu va contine elemente din alta parte a partitiei, pentru ca daca subsecventa se intinde pe mai multe parti, atunci putem elimina prefixul subsecventei care reprezinta o parte a partitiei, acea parte avand suma negativa.

sum = -infinit; bestSum = -infinit;
for (i = 1; i <= N; i++) {
      sum += a[ i ];
      if (sum < 0) {
         sum = 0;
         continue;
      } else if (sum >= bestSum) bestSum = sum;      
}

Problema 2 (Maximum Sum) - 104 acm.uva.es

Se da o matrice de dimensiuni NxN cu elemente intregi. Se cere determinarea unei submatrici a carei elemente au suma maxima.

Exemplu

Pentru matriceasubmatricea de sumă maximă este următoarea:

Rezolvare

Putem folosi trucul construirii sumelor partiale prezentat in rezolvarea anterioara, pentru cazul 2D. Pastram in sum[i][j] suma tuturor elementelor a[i₁][j₁] cu proprietatea ca 1 <= i₁ <= i, si 1 <= j₁ <= j. Putem calcula sumele prin metoda programarii dinamice (complexitate O(N²)) folosind formula sum[i][j] = a[i][j] + sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1]. Acum pentru a calcula suma elementelor din matricea cu colturile (i₁, j₁), (i₂, j₂), unde i₁ <= i₂ si j₁ <= j₂ este suficient sa facem calculul sum[i₂][j₂] - sum[i₁-1][j₂] - sum[i₂][j₁-1] + sum[i₁-1][j₁-1]. Astfel putem evalua suma din fiecare submatrice in timp constant, deci rezolvarea are ordinul de complexitate O(N⁴).
O alta idee ar fi ca pentru fiecare pereche (i₁, i₂) fixate sa determinam perechea optima (j₁, j₂). Daca avem liniile i₁ si i₂ fixate atunci problema se transforma din una bidimensionala in una unidimensionala. Astfel pentru fiecare coloana j vom considera b[j] ca suma a elementelor a[i][j] cu proprietatea ca i₁ <= i <= i₂. In exemplul nostru daca i₁ = 2 si i₂ = 3, atunci avem b₁ = 9 + (-4), b₂ = 2 + 1, b₃ = (-6) + (-4) si b₄ = 2 + 1. Pentru a rezolva problema unidimensionala folosim unul din algoritmii liniari prezentati mai sus, astfel obtinandu-se un algoritm de complexitate totala O(N³). Acest truc de a fixa doua linii pentru a transforma problema in una unidimensionala este util in multe probleme pe matrice sau cu puncte in plan.
Cel mai bun algoritm cunoscut pentru aceasta problema are complexitatea 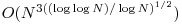si este mai mult un algoritm teoretic decat unul practic, usor implementabil.