Revizia anterioară Revizia următoare
Probleme cu secvenţe
(Categoria Diverse, autor Cosmin Negruşeri)
- Cuprins
- Introducere
- Problema 1 ( Subsecvenţa de sumă maximă )
- Problema 2 ( Maximum Sum )
- Problema 3 ( Interogare )
- Problema 4
- Problema 5
Introducere
Acest articol prezintă o serie de probleme înrudite cu problema subsecvenţei de sumă maximă, însoţite de rezolvări eficiente. Problemele prezentate pot apărea oricând ca subprobleme în concursurile de programare, studierea lor mărind în mod util bagajul de cunoştinţe al unui elev pasionat de algoritmică.
Problema 1 ( Subsecvenţa de sumă maximă )
Se dă un şir de N numere întregi (a1, a2, ..., aN). Să se determine o subsecvenţă (ai, ai+1, ..., aj) care să aibă suma maximă.
Exemplu
Pentru secvenţa de numere (-1, 2, 3, -4, -2, 2, 1, -3, -2, -3, -4, 9, -2, 1, 7, 8, -19, -7, 2, 4, 3), o subsecvenţă de sumă maximă este (9, -2, 1, 7, 8).
Rezolvare
Prima rezolvare care ne vine în minte are complexitatea O(N3) şi constă în determinarea sumei fiecărei subsecvenţe posibile şi reţinerea maximului acestor sume. Este evident că anumite sume parţiale sunt calculate de mai multe ori.
Putem reduce complexitatea la O(N2) ţinând cont de faptul că suma subsecvenţei a[i..j] este egală cu suma subsecvenţei a[i..j-1], la care se adună a[j]. Păstrăm într-un şir sum[i] - suma elementelor din subsecvenţa a[1..i]. Pentru a determina suma elementelor din subsecvenţa a[i..j] facem diferenţa sum[i] - sum[j-1].
Ideea poate fi rafinată calculând pentru fiecare indice i numărul best[i], reprezentând subsecvenţa de sumă maximă cu capătul drept în i. Este uşor de observat că best[i] = max(sum[i] - sum[j-1]), unde j ia valori de la 1 la i. Relaţia anterioară se mai poate scrie best[i] = sum[i] - min(sum[j-1 ]). Obţinem astfel un algoritm liniar care ne determină subsecvenţa de sumă maximă cerută.
sum[0] = 0;
for (i = 1; i <= N; i++) sum[i] = a[i] + sum[i-1];
min = sum[0];
bestSum = -INFINIT;
for (i = 1; i <= N; i++) {
best[i] = sum[i] - min;
if (min > sum[i]) min = sum[i];
if (bestSum < best[i]) bestSum = best[i];
}O altă metodă de calcul poate fi dedusă folosind paradigma Divide Et Impera. La fiecare pas împărţim şirul în jumătate şi aflăm subsecvenţele de sumă maximă din cele două jumătăţi. După aceea trebuie să găsim subsecvenţa de sumă maximă ce are un capăt în fiecare din cele două jumătăţi ale sirului. Pentru aceasta alipim sufixul de sumă maximă a primei jumătăţi cu prefixul de sumă maximă a celei de-a doua.
int getMaxSubsequence(int l, int r) {
if (l == r) return a[l];
mid = (l + r) / 2;
bestL = getMaxSubsequence(l, mid);
bestR = getMaxSubsequence(mid + 1, r);
suf = 0;
pre = 0;
maxSuf = -INFINIT;
maxPre = -INFINIT;
for (i = mid; i >= l; i--) {
suf += a[i];
if (maxSuf < suf) maxSuf = suf;
}
for (i = mid + 1; i <= r; i++) {
pre += a[i];
if (maxPre < pre) maxPre = pre;
}
return max(bestL, max(bestR, maxPre + maxSuf));
}O idee bazată pe paradigma programării dinamice ar fi să folosim un şir best[ i ], reprezentând suma maximă a unei subsecvenţe ce se termină în a[i]. Problema se rezolvă cu următoarea formulă de recurenţă: best[i] = max(a[i], best[i-1] + a[i]). Formula poate fi demonstrată prin inducţie matematică.
O ultimă idee ar fi să partiţionăm şirul în subsecvenţe încât fiecare să aibă ambele capete cât mai mici posibile şi suma elementelor subsecvenţei să fie negativă. Pentru exemplul dat avem următoarea partiţionare [-1], [2, 3, -4, -2], [2, 1, -3, -2], [-3], [-4], [9, -2, 1, 7, 8, -19, -7], [2, 4, 3]. O subsecvenţă de sumă maximă va avea primul capăt la începutul unei astfel de subsecvenţe, acest lucru explicându-se prin faptul că în caz contrar secvenţa poate fi mărită în stânga (orice secvenţă din cele alese pentru partiţionare are toate prefixele de sumă pozitivă, în afară de prefixul ce reprezintă întreaga subsecvenţă). De asemenea, orice subsecvenţă de sumă maximă nu va conţine elemente din altă parte a partiţiei, pentru că dacă subsecvenţa se întinde pe mai multe părţi, atunci putem elimina prefixul subsecvenţei care reprezintă o parte a partiţiei, acea parte având suma negativă.
sum = -INFINIT;
bestSum = -INFINIT;
for (i = 1; i <= N; i++) {
sum += a[i];
if (sum < 0) {
sum = 0;
continue;
} else
if (sum >= bestSum) bestSum = sum;
}Problema 2 ( Maximum Sum )
Se dă o matrice de dimensiuni NxN cu elemente întregi. Se cere determinarea unei submatrici a cărei elemente au suma maximă.
Exemplu
Pentru matricea![\[ \left( \begin{array}{cccc}0 & -2 & -7 & 0 \9 & 2 & -6 & 2 \-4 & 1 & -4 & 1 \-1 & 8 & 0 & -2 \end{array} \right)\] \[ \left( \begin{array}{cccc}0 & -2 & -7 & 0 \9 & 2 & -6 & 2 \-4 & 1 & -4 & 1 \-1 & 8 & 0 & -2 \end{array} \right)\]](http://www.infoarena.ro/static/images/latex/4803085c25ba4c147f20981b47e7b734_22.50023pt.gif) submatricea de sumă maximă este următoarea:
submatricea de sumă maximă este următoarea:![\[ \left( \begin{array}{cc}9 & 2 \-4 & 1 \-1 & 8 \end{array} \right)\] \[ \left( \begin{array}{cc}9 & 2 \-4 & 1 \-1 & 8 \end{array} \right)\]](http://www.infoarena.ro/static/images/latex/c9c94ab8a91b4daa70fdabcf22db7651_16.50017pt.gif)
Rezolvare
Putem folosi trucul construirii sumelor parţiale din rezolvarea anterioară, pentru cazul 2D. Păstrăm în sum[i][j] suma tuturor elementelor a[i1][j1] cu proprietatea că 1 <= i1 <= i, şi 1 <= j1 <= j. Putem calcula sumele prin metoda programării dinamice (complexitate O(N2)) folosind formula sum[i][j] = a[i][j] + sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1]. Acum pentru a calcula suma elementelor din matricea cu colţurile (i1, j1) şi (i2, j2), unde i1 <= i2 şi j1 <= j2, este suficient să facem calculul sum[i2][j2] - sum[i1-1][j2] - sum[i2][j1-1] + sum[i1-1][j1-1]. Astfel putem evalua suma din fiecare submatrice în timp constant, deci rezolvarea are ordinul de complexitate O(N4).
O altă idee ar fi ca pentru fiecare pereche (i1, i2) fixată să determinăm perechea optimă (j1, j2). Dacă avem liniile i1 şi i2 fixate atunci problema se transformă din una bidimensională în una unidimensională. Astfel pentru fiecare coloană j vom considera b[j] ca sumă a elementelor a[i][j] cu proprietatea că i1 <= i <= i2. În exemplul nostru, dacă i1 = 2 şi i2 = 3, atunci avem b1 = 9 + (-4), b2 = 2 + 1, b3 = (-6) + (-4) şi b4 = 2 + 1. Pentru a rezolva problema unidimensională folosim unul din algoritmii liniari prezentaţi mai sus, astfel obţinându-se un algoritm de complexitate totală O(N3). Acest truc de a fixa două linii pentru a transforma problema în una unidimensională este util în multe probleme pe matrice sau cu puncte în plan.
Cel mai bun algoritm cunoscut pentru această problemă are complexitatea 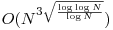 şi este mai mult un algoritm teoretic decât unul practic, uşor implementabil.
şi este mai mult un algoritm teoretic decât unul practic, uşor implementabil.
Problema 3 ( Interogare - Bursele Agora 2005/2006 Runda 1 )
Se consideră un şir A = (a1, a2, ..., aN), format din numere întregi (-100.000 <= ai <= 100.000), şi M perechi de numere (x, y) (1 <= N, M <= 100.000). Pentru fiecare pereche ordonată de indici (x, y) trebuie determinată subsecvenţa de sumă maximă a subşirului ax, ax+1, ..., ay. Subsecvenţele alese trebuie să conţină cel puţin un element.
Exemplu
Pentru şirul (-1, 2, 3, -2, 4, -3, 8, -3, 1) şi intervalele [1, 5], [4, 8] si [6, 6] avem soluţiile:
- 7 pentru subsecvenţa (-1, 2, 3, -2, 4);
- 9 pentru subsecvenţa (-2, 4, -3, 8, -3);
- -3 pentru subsecvenţa (-3).
Rezolvare
Putem obţine un algoritm de complexitate O(MN) folosind algoritmii liniari din prima problemă, dar să vedem cum putem reduce complexitatea folosind alte abordări. Mai întâi calculăm şirul sum al sumelor parţiale, după care împărţim şirul în k subsecvenţe de lungimi egale [n/k], şi păstrăm următoarele informaţii pentru fiecare din ele:
- max[i] - cea mai mare valoare sum[j], unde n/k * (i-1) < j <= n/k * i;
- min[i] - cel mai mic sum[j-1], unde n/k * (i-1) < j <= n/k * i;
- best[i] - valoarea subsecventei de suma maxima a secventei curente.
Acum, pentru a afla subsecvenţa de sumă maximă a subsecvenţei a[x..y] studiem cele două cazuri posibile:
1. Dacă elementele de indice x şi y aparţin aceleiaşi subsecvenţe, atunci putem găsi ceea ce căutăm folosind algoritmul liniar direct pe şirul a[x..y] (complexitate O(n/k)).
2. Dacă nu sunt în aceeaşi secvenţă, atunci vom împărţi şirul a[x..y] în:
- un prefix de subsecvenţă din cele ce aparţin partiţionării,
- un sufix de subsecvenţă,
- zero sau mai multe subsecvenţe complete ce aparţin partiţionării,
după care rezolvăm problema pentru sufix şi prefix prin metoda liniară ( O(n/k) ), şi determinăm în O(1) pentru fiecare bucată în care este spart şirul a[x..y] subsecvenţa ei de sumă maximă.
Mai rămâne să găsim subsecvenţa de sumă maximă cu capătul în bucăţi diferite. Pentru două bucăţi fixate i <= j, subsecvenţa de sumă maximă ce are câte un capăt în fiecare bucatăm are valoarea max[j] - min[i]. Determinarea subsecvenţei de sumă maximă cu capetele în bucăţi diferite devine astfel de complexitate O(k). Deci pentru a rezolva o întrebare trebuie să facem O(n/k + k) calcule. Pentru a reduce complexitatea problemei considerăm pe k = sqrt(n). Complexitatea totală a acestei soluţii este O(N + M sqrt(N)).
Să vedem ce se întâmplă pe exemplu:
| a | - | -1 | 2 | 3 | -2 | 4 | -3 | 8 | -3 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| sum | 0 | -1 | 1 | 4 | 2 | 6 | 3 | 11 | 8 | 9 |
Şirul e împărţit în trei subsecvenţe [-1, 2, 3], [-2, 4, -3], [8, -3, 1]:
| max | 4 | 6 | 11 |
|---|---|---|---|
| min | -1 | 2 | 8 |
| best | 5 | 4 | 8 |
Pentru a răspunde la întrebarea [1, 5] trebuie să răspundem la cele două subsecvenţe componente [1..3] şi [4..5]. Soluţia optimă pentru [1..3] este best1 = 5. Soluţia optimă pentru [4..5] o determinăm folosind algoritmul liniar, ea fiind 4. Acum, pentru a determina subsecvenţa de sumă maximă cu câte un capăt în fiecare interval folosim formula max(sum[i]) - min(sum[j-1]), unde 4 <= i <= 5 şi 1 <= j <= 3. Valoarea max(sum[i]) o găsim parcurgând intervalul [4, 5] ca fiind 6, iar valoarea min(sum[j-1]) o avem deja calculată în min1. De aici obţinem rezultatul 7.
O soluţie similară poate fi obţinută cu ajutorul arborilor de intervale. Mai întâi creăm arborele de intervale. Pentru fiecare interval aflăm elementele min, max şi best astfel:
- min[x..y] = minim(min[x..(x+y)/2], min[(x+y)/2 + 1 .. y]);
- max[x..y] = maxim(max[x..(x+y)/2], max[(x+y)/2 + 1 .. y]);
- best[x..y] = maxim(best[x..(x+y)/2], maxim(best[(x+y)/2 + 1 .. y], max[(x+y)/2 + 1 .. y] - min[x..(x+y)/2])).
Acum pentru a răspunde la întrebările din problemă fiecare interval va fi împărţit în O(log N) subintervale canonice care apar în arborele de intervale. Apoi printr-o parcurgere asemănătoare celei din rezolvarea anterioară se poate obţine rezultatul pentru fiecare întrebare în O(log N). Soluţia va avea complexitatea O(N + M log N).
În următorul desen observăm structura unui arbore de intervale pentru un şir cu 16 elemente. Daca se pune întrebarea [2, 11] acest interval va fi spart în intervalele [2, 2], [3, 4], [5, 8], [9, 10], [11, 11].
Prezentăm procedura de construire a arborelui, implementată în java:
public void build_tree(int index, int low, int high) {
if (low == high) {
if (low != 0) aint[index] = new Node(low, high, a[low] - a[low - 1], a[low], a[low]);
else aint[index] = new Node(low, high, 0, 0, 0);
}
else {
aint[index] = new Node(low, high, -INFINIT, -INFINIT, INFINIT);
int mid = (low + high) / 2;
build_tree(2 * index, low, mid);
build_tree(2 * index + 1, mid + 1, high);
aint[index].maxS = Math.max(aint[2 * index].maxS,Math.max(aint[2 * index + 1].maxS,aint[2 * index + 1].max - aint[2 * index].min));
aint[index].max = Math.max(aint[2 * index].max,aint[2 * index + 1].max);
aint[index].min = Math.min(aint[2 * index].min,aint[2 * index + 1].min);
}
}Şi procedura care răspunde la întrebări tot în java:
long minPrefix;
int x, y;
public long queryTree(int index, int low, int high) {
if (x <= low && high <= y) {
long maxRet = aint[index].maxS;
if (minPrefix != infinity) {
maxRet = Math.max(maxRet, aint[index].max - minPrefix);
}
minPrefix = Math.min(minPrefix, aint[index].min);
return maxRet;
}
else {
int mid = (low + high) / 2;
if (x <= mid && mid < y) return Math.max(queryTree(2 * index, low, mid), queryTree(2 * index + 1, mid + 1, high));
else if (x > mid) return queryTree(2 * index + 1, mid + 1, high);
else return queryTree(2 * index, low, mid);
}
}Problema 4 ( ACM ICPC NWERC 97, olimpiada online 2000, campion 2001 )
Se dă un şir (a1, a2, ..., aN) format din numere întregi. Se cere să se determine subsecvenţa a[i..j] care are modulul sumei elementelor minim.
Exemplu
Pentru şirul (2, 8, -6, -6, 9, 4, -3), subsecvenţa este (4, -3), având suma în modul 1 = |4 - 3|.
Rezolvare
Facem mai întâi şirul sumelor parţiale. Pentru oricare două elemente sum[i] şi sum[j] ($i != j$) modulul sumei unei subsecvenţe din şir va fi |sum[i] - sum[j]|. Dacă i < j, atunci secvenţa va fi a[i+1..j], iar dacă j < i, atunci secvenţa va fi a[j+1 .. i]. Astfel, pentru a găsi subsecvenţa de modul minim trebuie, de fapt, să găsim perechea de indici i şi j astfel ca |sum[i] - sum[j]| să fie minim. Sortând şirul sumelor parţiale şi luând o pereche de indici i < j, atunci sum[i] < sum[j], iar |sum[j] - sum[i]| = sum[j] - sum[i]. Pentru a găsi perechea (i, j) pentru care i < j şi sum[j] - sum[i] este minim, trebuie ca i să fie egal cu j + 1. Astfel obţinem un algoritm de complexitate O(N log N).
Să vedem cum merge pe exemplul prezentat:
| a | - | 2 | 8 | -6 | -6 | 9 | 4 | -3 |
|---|---|---|---|---|---|---|---|---|
| sum | 0 | 2 | 10 | 4 | -2 | 7 | 11 | 8 |
| ind | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
În şirul ind vom păstra indicii reali ai sumelor parţiale. După sortare avem:
| sum | -2 | 0 | 2 | 4 | 7 | 8 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|
| ind | 4 | 0 | 1 | 4 | 5 | 7 | 2 | 6 |
O secvenţă de modul 2 ar fi cea reprezentată de sumele 8 şi 10, cu indicii 7 şi 2. Această secvenţă este (-6, -6, 9, 4, -3). Observăm ca cea mai mică diferenţă între termeni consecutivi e cea dintre 8 şi 7, care au indicii 7 şi 5, de unde obţinem că subsecvenţa de modul minim este (4, -3).
Problema 5 - USACO
Se da un sir (a1, a2, ..., aN) format din N (1 <= N <= 100 000) numere intregi ($1 <= ai <= 2 000$). Se cere sa se determine subsecventa a[i..i + K - 1] cu media aritmetica a elementelor maxima ( K >= F, 1 <= F <= N).
Exemplu
Pentru sirul (6, 4, 2, 10, 3, 8, 5, 9, 4, 1) si F = 6 soluţia optima este (10, 3, 8, 5, 9, 4), cu media 6.5.
Rezolvare
Fie X un numar real. Daca obtinem sirul b prin transformarea bi = ai - X, atunci toate subsecventele sirului b vor avea valoarea mediei elementelor lor cu X mai mica decat valoarea subsecventelor corespunzatoare din sirul a. Daca subsecventa de suma maxima din b are valoarea mai mare ca 0, atunci si media ei va fi mai mare ca 0. Rezulta astfel ca si media subsecventei corespunzatoare din sirul a va fi mai mare decat X, deci media maxima a unei subsecvente din a va fi mai mare ca X. Cand subsecventa de suma maxima din sirul b are media mai mica decat zero, atunci orice subsecventa din sirul a va avea media mai mica decat X. Iar in cazul in care subsecventa de suma maxima a sirului b are valoarea egala cu zero, atunci subsecventa de medie maxima a sirului a are media X. Astfel putem face o cautare binara pentru a determina valoarea X a mediei maxime. Ne mai ramane sa determinam un algoritm eficient pentru gasirea subsecventei de suma maxima de lungime cel putin F.
O asemenea solutie este usor de facut urmarind una din ideile din prima problema: fie best[i] subsecventa de suma maxima care se termina in a[i]. Evident best[i] = max(a[i], best[i - 1] + a[i]). Acum secventa de suma maxima ce se termina in a[i] de lungime cel putin F se gaseste ca a[i] + a[i - 1] + .. + a[i - F + 2] + best[i - F + 1]. Aceasta relatie poate fi calculata in O(1) daca ne folosim de trucul sumelor partiale.
Astfel obtinem o solutie de complexitate O(N log C), unde C e valoarea maxima a lui $ai.
