Probleme cu puncte laticiale

(Categoria Matematică, Autor Cosmin Negruşeri)

• Conţinut
• Introducere
• Problema 1
• Problema 2
• Problema 3: Copaci
• Problema 4
• Problema 5: Counting triangles
• Problema 6: Dreptunghiuri
• Problema 7: Paralelograme
• Concluzii
• Bibliografie

Introducere

Articolul de faţă se va concentra pe probleme în care vor apărea puncte de coordonate întregi care sunt numite puncte laticiale. Sursele [1] şi [2] menţionate în bibliografie conţin câte un capitol despre puncte laticiale care, deşi sunt mai matematice decât acest articol, pot fi interesante pentru un elev în pregătirea pentru olimpiadă. Să vedem acum câteva probleme ce au apărut pe la concursurile de programare.

Problema 1

Să se determine numărul de puncte de coordonate întregi prin care trece segmentul determinat de punctele (0, 0) şi (M, N). De exemplu, pentru M=9 şi N=12 pe segment vor fi 4 puncte de coordonate întregi.

Rezolvare

Putem considera doar cazurile în care 0 ≤ N ≤ M, dacă N = 0 atunci evident avem M+1 puncte pe segment. Astfel trebuie să rezolvăm doar cazul în care 1 ≤ N ≤ M.
Evident că orice punct (x, y), pentru a fi pe segmentul nostru, trebuie să satisfacă ecuaţia y=M/N*x. Această ecuaţie are ca soluţie un număr natural doar dacă M*x se divide cu N, de aici dacă D=cmmdc(N, M) atunci x se divide cu N/D, deci x de forma k*N/D => y=k*M/D. Pentru ca punctul (x, y) să aparţină segmentului, trebuie ca 0 ≤ x ≤ N şi 0 ≤ y ≤ M astfel 0 ≤ k ≤ D. Deci numărul de puncte de pe un segment de la (0, 0) la (N, M) este egal cu cel mai mare divizor comun al numerelor M şi N la care adăugăm 1. Putem determina acest număr în complexitate O(log (N + M)).

Problema 2

Se dă un triunghi cu vârfurile de coordonate întregi. Se cere să se determine numărul de puncte de coordonate întregi ce se află în interiorul triunghiului sau pe laturile lui. De exemplu un triunghi cu vârfurile de coordonate (1, 5), (5, 1) şi (6, 6) are 16 puncte în interior.

Rezolvare

Pentru un dreptunghi cu laturile paralele cu axele de coordonate de lungime M şi lăţime N avem că numărul de puncte situate strict în interiorul dreptunghiului este (M–1)×(N–1), iar numărul de puncte situate pe laturile poligonului este 2M + 2N. Dacă notăm cu B numărul de puncte de pe laturi, cu I numărul de puncte situate strict în interiorul unui dreptunghi şi cu A aria dreptunghiului, observăm că I+B/2–1 = (M–1)×(N–1)+M+N–1 = M×N = A.
În cazul triunghiurilor dreptunghice ce au două catete vom vedea că această formulă se păstrează. Evident avem că A = (M×N)/2. Pe ipotenuza triunghiului vom avea D puncte (D = cmmdc(M, N)+1, dar aceasta nu ne interesează pe moment), deci numărul de puncte de pe laturile triunghiului este B = M+N+D–1. Numărul de puncte I din interiorul triunghiului este numărul de puncte din interiorul dreptunghiului ×(N-1) din care se scad punctele interioare de pe diagonala D–2, rezultatul împărţindu-se apoi la 2, de aici avem I = ((M-1)×(N-1)–D+2)/2.
Verificăm formula I+B/2–1 = (M-1)×(N-1)/2–D/2+1+M/2+N/2+D/2+1/2 = (M×N)/2.
Deci formula se verifică şi pe astfel de triunghiuri.
Acum ne uităm la cel mai mic dreptunghi ce conţine un triunghi oarecare, acest dreptunghi poate fi împărţit în patru triunghiuri din care unul este cel iniţial, iar celelalte sunt trei triunghiuri dreptunghice pentru care catetele merg de-a lungul liniilor laticiale. Vom vedea că formula noastră se verifică şi pentru triunghiuri oarecare. Notăm cu I_d numărul de puncte înterioare dreptunghiului, A_d aria dreptunghiului şi B_d numărul de puncte de pe laturile dreptunghiului, cu I₁, I₂, I₃ numărul de puncte din interiorul celor trei triunghiuri dreptunghice, B₁, B₂, B₃ numărul de puncte de pe laturile celor trei triunghiuri, iar A₁, A₂ şi A₃ ariile celor trei triunghiuri. Avem că I = I_d–I₁–I₂–I₃–B+3 (trebuie să eliminăm punctele de pe laturile triunghiului interior şi să avem grijă de vârfurile acestui triunghi), B = B₁+B₂+B₃–B_d iar A = A_d–A₁–A₂–A₃. De aici avem că I+B/2–1 = I_d–I₁–I₂–I₃ - B₁/2-B₂/2-B₃/2+B_d/2–1+3 = (I_d+B_d/2–1)–(I₁+B₁/2–1) - (I₁+B₁/2–1)-(I₁+B₁/2–1) = A_d–A₁–A₂–A₃ = A, deci egalitarea este valabilă şi pentru triunghiuri oarecare.

Acum aria triunghiului cu vârfurile (x1, y1), (x2, y2), (x3, y3) o putem afla uşor folosind formula lui Heron sau folosind

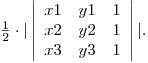
Numărul de puncte de pe laturile triunghiului poate fi determinat uşor folosind formula demonstrată în problema anterioară. Acum folosind formula I+B/2–1 = A putem afla numărul I şi problema e rezolvată prin întoarcerea numărului I+B. Complexitatea rezolvării este O(log N) unde N este valoarea maximă a coordonatelor.

Problema 3 Copaci (infoarena)

Macarie, după ce a muncit o viaţă întreagă, se decide la bătrâneţe să se retragă pe o insulă pentru a-şi găsi liniştea interioară şi a se dedica naturii. Astfel el cumpără o insula pe care cultivă pomi fructiferi. Insula poate fi reprezentată ca un poligon (nu neaparat convex) într-un sistem de axe de coordonate pozitive. Pomii sunt plantaţi doar la coordonate naturale.
Macarie este interesat de numărul de copaci pe care îl poate planta strict in interiorul insulei. În acest scop el va furnizează copacii care determina insula (vârfurile poligonului).
De exemplu pentru poligonul dat prin vârfurile (0, 4), (0, 5), (2, 7), (2, 4), (6, 6) şi (4, 0) avem 12 puncte de coordinate întregi situate strict în interiorul poligonului.

Rezolvare

Formula I+B/2–1 = A prezentată mai sus se numeşte Teorema lui Pick, iar ea este valabilă şi pentru poligoane oarecare. Acest fapt este adevărat pentru că orice poligon are o diagonală înterioară, această diagonală îl împarte în două poligoane distincte, dacă notăm I₁ şi I₂ punctele interioare celor două poligoane, B₁ şi B₂ punctele de pe laturile celor două poligoane, A₁ şi A₂ laturile celor două poligoane şi D numărul de puncte de cooronate întregi de pe diagonală atunci dacă egalitatea ar fi fost satisfăcută pentru cele două poligoane atunci avem că B₁+B₂ = B+2D-2, I = I₁+I₂+D–2. De aici avem A = A₁+A₂ = I₁+B₁/2–1+I₂+B₂/2-1 = I₁+I₂+B/2+D–1–2 = I+B/2–1. Astfel putem demonstra prin inducţie că relaţia este satisfăcută pentru orice poligon.
Aria unui poligon poate fi calculată uşor folosind următoarea formulă
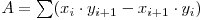, unde punctul de indice n+1 este primul punct. Astfel obţinem un algoritm de complexitate O(N log (MaxX + MaxY)).

Problema 4 (Marele Premiu Paco 2000)

Se dă o grilă de puncte laticeale de dimensiuni N × N, se cere să se determine numărul de pătrate care se pot forma astfel ca vârfurile lor să aparţină punctelor din grilă.
De exemplu pe o grilă de dimensiuni 3 × 3 există 6 pătrate.

Rezolvare:

Un pătrat cu latură ce conţine L puncte, ce are laturile paralele cu axele de coordonate poate fi translatat în (N–L+1)×(N–L+1) poziţii diferite pe grila noastră.

Considerăm pentru un pătrat din mulţimea soluţiilor, dreptunghiul minim cu laturile paralele cu axele de coordonate ce conţine acest pătrat. Este uşor să vedem că acest dreptunghi este de fapt un pătrat. Într-un pătrat ce are L puncte pe latura înscrie L – 2 pătrate care nu au laturile paralele cu axele de coordonate.

Astfel vedem că numărul total de pătrate pe o grilă N × M este:

Sumă după L de la 2 la N de (N–L+1) × (N–L+1) × (L–1) =
suma L de la 1 la N-1 de (N–L) × (N–L) × L = suma cu L de la 1 la N–1 de LN²–2 NL² + L³ = N² × suma L de la 1 la N-1-2N suma L de la 1 la N–1 de L² + suma de L de la 1 la N–1 de L³ = N² × N(N-1)/2-2N n(n-1)(2n-1)/6 + [n(n-1)/2]².

Am folosit formulele cunoscute din manualul de clasa a 10-a:




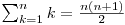
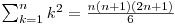
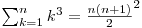
Această soluţie are complexitatea O(1), fiind o simplă formulă.

Problema 5 Counting triangles (ACM ICPC Asia – Dhaka 2005/2006)

Triunghiurile sunt poligoane cu trei laturi şi cu aria strict pozitivă. Triunghiurile laticiale sunt triunghiuri ce au vârfurile de coordonate întregi. În această problemă va trebui să găsiţi numărul de triunghiuri laticiale ce se pot găsi pe o grilă de dimensiuni M×N (1 ≤ M, N ≤ 1000). De exemplu pe o grilă de dimensiuni 1×2 găsim 18 triunghiuri laticiale distincte după cum vedem în figură:

Rezolvare

Prima idee de rezolvare ar fi de a lua toate combinaţiile de trei puncte distincte dintre cele N×M puncte şi apoi de a elimina oricare trei puncte colineare, dar partea a doua pare greu de realizat în mod eficient.
Vom număra asemănător rezolvării de mai sus numărul de triunghiuri înscrise într-un dreptunghi paralel cu axele de coordonate. Apoi acel dreptunghi îl vom putea translata pe grila de puncte laticiale şi astfel vom putea număra toate triunghiurile posibile.

Oricum ar fi un triunghi situat într-un dreptunghi ce este minimal, cel putin un vârf al triunghiului trebuie să fie un vârf al dreptunghiului. Se disting astfel două cazuri: primul în care un vârf al triunghiului este şi vârf al dreptunghiului şi celelalte două puncte sunt situate pe cele două laturi ale dreptunghiului ce nu au ca şi capăt primul punct, iar al doilea caz în care cel puţin două vârfuri sunt vârfuri ale dreptunghiului opuse pe diagonală. Dacă dreptunghiul are H puncte pe verticală şi W puncte pe orizontală, atunci în primul caz vom avea 4 × ((H–1) × (W–1) + H–1 + W-1) triunghiuri, iar în al doilea caz vom avea 2 × (H × W - X) unde X e numărul de puncte de coordonate întregi de pe diagonala dreptunghiului. Cum trebuie să numărăm triunghiurile înscrise în fiecare dreptughi pt care 1 ≤ H ≤ N şi 1 ≤ W ≤ M, obţinem un algoritm de complexitate O(NM log N), acel log N apare la calcularea lui X.

Problema 6 Dreptunghiuri (preOni 2006 runda 1)

Clod stă într-o zi plictisit la ora de matematică şi în timp ce profesorul explică la tablă teorema lui Pick, Clod se gândea la o problemă mai interesantă: pentru o grilă de puncte laticiale de dimensiune N×M (0 < M, N ≤ 400) care este numărul de dreptunghiuri cu vârfurile în puncte laticiale. Clod este curios dacă există o formulă pentru această problemă şi ar vrea să ştie soluţia pentru diferite dimensiuni ale grilei, pentru a putea ghici o asemenea formulă.
Ajutaţi-l pe Clod să afle răspunsul!

De exemplu pentru o grilă de 3×3 puncte găsim 10 dreptunghiuri.

Rezolvare

Un dreptunghi care apare în grila de puncte laticiale este mărginit de două drepte verticale la stânga şi la dreapta, şi de două drepte orizontale în sus şi în jos. Acum, dacă vrem pentru patru drepte fixate să ştim câte dreptunghiuri mărginesc ele, ne putem uita la următorul desen.

Dacă dreptunghiul ABCD determinat de cele patru drepte are vârfurile laturile H şi W atunci un dreptunghi MNPQ înscris va împărţi laturile lui in bucăţile AM, MB şi AQ, QD. Evident dacă MNPQ este dreptunghi atunci avem că AM=PC, MB=PD, AQ=NC şi QD=NB. Fie M’ proiecţia punctului M pe latura DC. Acum folosind teorema lui Pitagora avem că:
AQ² + AM² = MQ²
QD² + DP² = QP²
MQ² + QP² = MP²
MM’² = (AQ + QD)²
M’P² = (PD - PC)²
MM’² + M’P² = MP²
De aici rezultă că (AQ + QD)² + (PD – PC)² = AQ² + DQ² + AM² + MB², astfel obtinem AQ×QD = AM×MA, dacă notăm cu A lungimea lui AM şi cu x lungimea lui AQ atunci avem că QD = H–A, iar MA = W–x deci avem că x^2 – W×x + A×(H–A) = 0. Dacă îl fixăm pe A atunci trebuie să rezolvăm o ecuaţie de gradul doi în necunoscuta x, soluţia trebuie să fie întreagă între 0 şi W.
Astfel in O(H) vom şti numărul de dreptunghiuri înscrise într-un dreptunghi de dimensiuni H×W. Acest dreptunghi poate fi pus in (N–H+1)×(M–H+1) locaţii pe o grilă de dimensiune N×M. Deci soluţia are complexitate O(N*M²), pentru fiecare dreptunghi de dimensiuni 1 ≤ H ≤ N şi 1 ≤ W ≤ M calculându-se numărul de dreptunghiuri înscrise.
O rezolvare de complexitate O(N²*M²) în care se căutau soluţiile ecuaţiei printr-un for ar fi luat 60 de puncte. Rezolvarea directă folosind ecuaţia de gradul doi ia în jur de 80 de puncte. Algoritmul poate fi optimizat la factorii constanţi, de exemplu avem nevoie de funcţia radical care este cam înceată, precalculând-o obţinem o accelerare a vitezei, altă idee ar fi că numărul de soluţii cu A ≤ H/2 este egal cu numărul de soluţii cu H – H/2 ≤ A şi a treia idee de optimizare este că numărul de dreptunghiuri înscrise într-un dreptunghi de dimensiuni H, W este acelaşi cu numărul de dreptunghiuri înscrise intr-un dreptunghi de dimensiuni W, H.

Problema 7 Paralelograme (Bursele Agora 2005/2006 runda 1)

Clod este din nou plictisit la ora matematică şi se joacă desenând pe o foaie cu pătrăţele paralelograme cu vârfurile în colţurile pătrăţelelor. Tot desenând paralelograme, Clod se întreabă câte astfel de paralelograme poate construi dacă ştie că foaia de pătrăţele are N linii şi M coloane (0 < N, M ≤ 2000).
Va trebui să îl ajutaţi să rezolve această problemă.
Pentru N=2 şi M=2 putem construi 22 de paralelograme

Rezolvare

Ca să determinăm numărul de paralelograme ce se pot găsi pe o grilă laticială, proprietatea că diagonalele unui paralelogram se înjumătăţesc pare să ne ajute în obţinerea unui algoritm de complexitate O(N + M), dar autorul nu a reuşit să numere într-un mod eficient câte paralelograme sunt degenerate (cu cele patru vârfuri colineare) pentru a putea să le eliminăm din numărul total.

Din nou putem folosi ideea celui mai mic dreptunghi cu laturile paralele cu axele de coordonate pentru a număra repede o clasă mare de paralelograme de aceiaşi formă.
Avem două cazuri posibile:

Primul în care cele patru puncte sunt pe laturile dreptunghiului iar nici un vârf nu coincide cu vârfurile dreptunghiului, şi al doilea în care există două puncte în vârfuri opuse ale dreptunghiului.
În primul caz, dacă avem poziţiile a două vârfuri fixate pe două laturi consecutive ale dreptunghiului, atunci poziţiile celorlator două vârfuri sunt unic determinate. De aici obţinem că în primul caz avem ×(w-2) paralelograme.
În al doilea caz dacă fixăm două vârfuri ale paralelogramului în colţurile dreptunghiului, celelalte două vârfuri vor fi simetrice faţă de centrul de greutate al dreptunghiului, trebuie să nu luăm în calcul posibilitatea ca vărfurile să fie pe diagonala dreptunghiului, de aici obţinem h * w - cmmdc(h-1, w-1) – 2 posibilităţi.

Astfel am ajuns la următorul algoritm:

long num = 0;
for (long h = 2; h <= N + 1; h++) 
  {for (long w = 2; w <= M + 1; w++) 
     {laux = (h - 2) * (w - 2) + h * w - cmmdc(h - 1, w - 1) - 2;
      num += (N - h + 1) * (M - w + 1) * laux;
     }
}

Acest algoritm are complexitatea O(NM log N), el nu s-ar fi încadrat în timpul impus, marea parte a calculelor este efectuată în determinarea celui mai mare divizor comun a două numere, având în vedere că numerele folosite sunt între 1 şi N respectiv între 1 şi M, putem să calculăm o matrice CMMDC[X][Y] unde 1 ≤ X ≤ N şi 1 ≤ Y ≤ M, această matrice poate fi calculată în O(NM). Astfel complexitatea soluţiei a fost redusă la $O(NM)$, mai putem optimiza factorii constanţi ai soluţiei observând că într-un triunghi de dimensiuni H×W pot fi înscrise acelaţi număr de dreptunghiuri ca şi într-un triunghi W×H, acest artificiu aproape dublează viteza algoritmului. Menţionăm că aceleaşi optimizări pot fi făcute şi la problema cu triunghiuri.

Concluzii

Cititorul poate să încerce aplicarea tehnicilor din articol la alte probleme similare, de exemplu determinarea numărului de patrulatere convexe nedegenerate cu vârfurile puncte laticiale, sau numărului de romburi sau trapeze.

Bibliografie

• Buşneag, Maftei, Teme pentru cercurile şi concursurile de matematică ale elevilor, Scrisul Românesc, Craiova, 1983
• Iaglom, Iaglom, Probleme neelementare tratate elementar, ed tehnică, Bucureşti, 1962
• WolframMathWorld
• FAQs
• Geometry Algorithms