| Fişierul intrare/ieşire: | wildcards.in, wildcards.out | Sursă | Lot Deva Seniori 2019, baraj 2 |
| Autor | Adrian Budau, Andrei Popa, Mihai Calancea | Adăugată de | |
| Timp execuţie pe test | 0.125 sec | Limită de memorie | 512000 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Wildcards
Numim pattern un şir nevid format doar din caracterele 0, 1 şi ?. Spunem că două patternuri A şi B de aceeaşi lungime se potrivesc dacă şi numai dacă caracterele ? pot fi înlocuite convenabil cu 0 şi 1 astfel încât cele două şiruri să devină identice. De exemplu, pentru A = “110?1”, B = “1?001”, C = “??1?1”, şirurile A şi B se potrivesc (se poate forma şirul “11001” prin înlocuirea semnelor de întrebare cu valori),
dar şirurile A şi C nu se potrivesc.
Se dă un arbore (graf neorientat conex aciclic) cu N noduri. Se cere să se atribuie fiecărui nod câte un şir format din caracterele 0, 1 şi ? (un pattern) astfel încât să se respecte următoarele proprietăţi:
- Toate patternurile să aibă aceeaşi lungime, care să fie cât mai mică (a se vedea rubrica Punctare).
- Pentru oricare două noduri distincte u şi v, patternurile asociate acestora se potrivesc dacă şi numai dacă există muchia (u, v) în arbore.
Date de intrare
Fişierul de intrare wildcards.in va conţine pe prima linie numărul de noduri din arbore N. Pe următoarele N - 1 linii fişierul va conţine câte două numere a şi b cu semnificaţia că există o muchie între a şi b.
Date de ieşire
Fişierul de ieşire wildcards.out va contine N linii, pe linia i aflandu-se patternul nodului i.
Punctaj
În concurs punctajul pe un subtask era minimul dintre scorurile obţinute la testele din subtaskul respectiv, dar datorită unor limitări tehnice, punctarea se va face in felul următor:
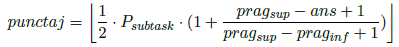
| Subtask | Punctaj | Constrangeri | |
|---|---|---|---|
| 1 | 6 puncte | 2 ≤ N ≤ 100, praginf = 100, pragsup = 100 | |
| 2 | 9 puncte | 2 ≤ N ≤ 10, praginf = 100, pragsup = 100 | |
| 3 | 5 puncte | 2 ≤ N ≤ 10000, praginf = 34, pragsup = 34, arborele este un lant de N noduri | |
| 4 | 5 puncte | 2 ≤ N ≤ 10000, praginf = 34, pragsup = 34, arborele este binar complet | |
| 5 | 35 puncte | 2 ≤ N ≤ 10, praginf = 101, pragsup = 200 | |
| 6 | 40 puncte | 2 ≤ N ≤ 10, praginf = 34, pragsup = 42 | |
Exemplu
| wildcards.in | wildcards.out | |
|---|---|---|
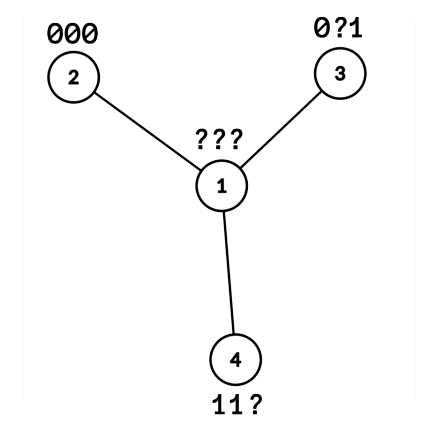
| 4 1 2 1 3 1 4 | ??? 000 0?1 11? | |
| 3 1 2 2 3 | 0 ? 1 | |
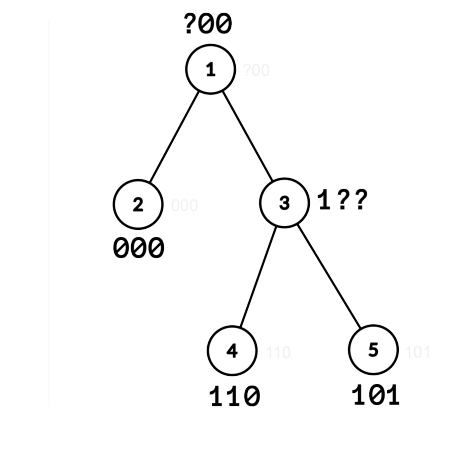
| 5 1 2 1 3 3 4 3 5 | ?00 000 1?? 110 101 | |
| 2 2 1 | ? ? | |
Explicaţie
Aceasta este figura pentru primul, respectiv cel de-al treilea exemplu: