| Fişierul intrare/ieşire: | vampir.in, vampir.out | Sursă | FMI No Stress 9 Warmup |
| Autor | Ioan Alexandru Tifui, Stelian Chichirim | Adăugată de |  FMI No Stress 9 •fminostress9 |
| Timp execuţie pe test | 0.1 sec | Limită de memorie | 16384 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Vampir
Daniel, aventuros din fire, a plecat intr-o excursie pe taramul vampirilor. Din nefericire, acesta a cazut prada unui vampir si acum se afla captiv in castelul acestuia. Harta taramului vampirilor poate fi reprezentata intr-un sistem de axe ortogonal, iar castelul in care se afla acum Daniel este plasat in origine. Se stie faptul ca pe taramul vampirilor exista o singura zona luminata de soare, care este sigura pentru oameni. Aceasta zona este reprezentata de conturul unui patrat ale carui diagonale se afla pe axele de coordonate. Se stie ca lungimea diagonalei patratului este L.
Dupa negocieri insistente, Daniel a reusit sa il convinga pe vampir sa il elibereze. Din nefericire, vampirul nostru este pasionat de matematica, in special de functia beta a lui Euler. Pentru doua numere naturle x si y,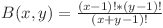 
. Asadar, vampirul ii pune la dispozitie lui Daniel un dispozitiv de teleportare care, pentru un numar K fixat, va putea transporta utilizatorul dintr-un punct (x1, y1) in alt punct (x2, y2), cu conditia ca 
, 
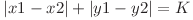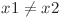si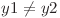 
. Pentru fiecare teleportate, Daniel va trebui sa ii plateasca vampirului un anumit cost. Costul unei teleportari din (x1, y1) in (x2, y2) il reprezinta 
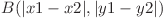. Deoarece Daniel uraste functia beta, acesta va alege la fiecare pas o teleportare cu cost minim. Daniel poate folosi mai multe teleportari pentru a ajunge in zona sigura, dar va folosi de fiecare data acelasi numar K. Inainte de plecare, Daniel se intreaba:
1) Care sunt valorile pare ale lui K pe care le poate alege pentru a ajunge in zona sigura folosind dispozitivul de teleportare
2) Care este costul minim pe care il va plati vampirului pentru a ajunge in zona sigura daca alege optim numarul par K
Date de intrare
Fişierul de intrare vampir.in contine pe prima linie doua numere naturale C si L. C poate avea valoarea 1 sau 2, in functie de intrebarea la care trebuie sa raspundeti, iar L are semnificati de mai sus.
Date de ieşire
Daca nu exista nicio valoare para K pe care Daniel sa o poata alege pentru a ajunge in zona sigura folosind dispozitivul de teleportare, atunci fişierul de ieşire vampir.out va contine pe prima linie numarul -1, indiferent de valoarea lui C.
In caz contrar:
In cazul in care C este 1 fişierul de ieşire vampir.out va contine pe prima linie numarul valorilor pare K pe care Daniel le poate alege pentru a ajunge in zona sigura folosind dispozitivul de teleportare.
Pe a doua linie, fisierul va contine in ordine crescatoare valorile pare ale lui K cu proprietatea de mai sus.
In cazul in care C este 2 fişierul de ieşire vampir.out va contine pe prima linie un singur numar, reprezentand costul minim pe care il va plati Daniel vampirului pentru a ajunge in zona sigura. Este garantat faptul ca acest numar se poate scrie ca o fractie ireductibila de forma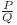 
. Se cere sa afisati valoarea P * Q-1 modulo 1000000007, unde Q-1 reprezinta inversul modular al lui Q in raport cu 1000000007.
Restricţii
- L este numar par
- 2 ≤ L ≤ 107
- Pentru teste in valoare de 50 de puncte C = 1
- Pentru alte teste in valoare de 50 de puncte C = 2
- Rezultatul la a doua cerinta trebuie afisat modulo 1000000007.
Exemplu
| vampir.in | vampir.out |
|---|---|
| 1 8 | 2 2 4 |
| 2 8 | 166666668 |
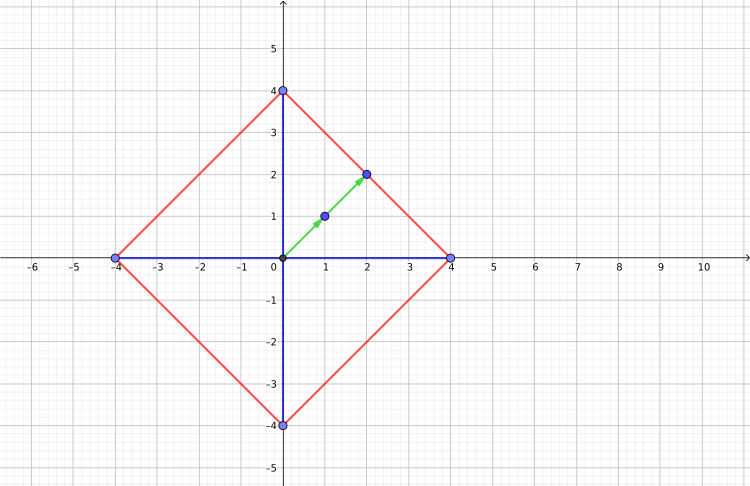
In primul exemplu, 2 si 4 sunt singurii k cu care se poate ajunge in zona sigura; cu k = 2 un posibil drum este: (0,0) -> (1,1) -> (2,2).
In al doilea exemplu, un posibil drum cu cost minim este cu k = 4 si drumul (0,0) -> (-2,-2), care are costul 1/6, deci se va afisa 1*6-1 modulo 1000000007.
In desenul de mai jos este ilustrat primul exemplu. Cu rosu este desenata zona luminata, iar cu verde drumul parcurs de Daniel.
