| Fişierul intrare/ieşire: | turnuri5.in, turnuri5.out | Sursă | Grigore Moisil 2018, 11-12 |
| Autor | Alex Cociorva, Bereczki Norbert Cristian, Mircea Popoveniuc | Adăugată de | |
| Timp execuţie pe test | 0.4 sec | Limită de memorie | 65536 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Turnuri5
La şcoală, Bulănel are de-a face cu următoarea problemă: i se dă o foaie ce conţine NxM puncte dispuse pe N linii şi M coloane. Liniile sunt numerotate începând de jos în sus, de la 0 la N-1, iar coloanele sunt numerotate începând de la stânga la dreapta, de la 0 la M-1.
Pe o astfel de foaie sunt marcate T turnuri. Turnurile au forma unor dreptunghiuri cu colţurile în punctele existente, cu baza pe linia 0. Fiecare turn i are câte o înălţime hi şi se întinde pe câte un interval de la li la ri pe coloane. Toate turnurile sunt disjuncte, adică nu au puncte în comun.
Bulănel îşi propune să deseneze dreptunghiuri pe foaia primită, însă acestea trebuie să fie valide. Dreptunghiurile valide trebuie să aibă arie strict mai mare decât 0, să aibă colţurile în punctele existente, să aibă laturile paralele cu marginile foii şi să nu aibă nici un punct comun cu niciunul din turnuri.
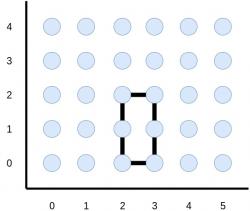
De exemplu, dacă Bulănel primeşte o foaie cu N=5 linii şi M=6 coloane şi un singur turn cu înălţime h1=2 care se întinde de la l1=2 la r1=3, atunci el poate desena dreptunghiuri cum ar fi:
- dreptunghiul care are colţul stânga sus pe linia 4, coloana 0 şi colţul dreapta jos pe linia 3, coloana 1.
- dreptunghiul care are colţul stânga sus pe linia 3, coloana 0 şi colţul dreapta jos pe linia 0, coloana 1.
În total el poate desena 33 de astfel de dreptunghiuri care respectă proprietăţile cerute.
El nu poate desena, de exemplu:
- dreptunghiul cu colţul stânga sus pe linia 4, coloana 0 şi colţul dreapta jos pe linia 1, coloana 4.
- dreptunghiul cu colţul stânga sus pe linia 4, coloana 0 şi colţul dreapta jos pe linia 2, coloana 2.
- dreptunghiul cu colţul stânga sus pe linia 4, coloana 0 şi colţul dreapta jos pe linia 2, coloana 4.
Bulănel vă cere să-l ajutaţi să numere câte dreptunghiuri valide poate desena pe foaia primită. Deoarece acest număr poate fi foarte mare, se cere sa se afişeze modulo 109 + 7.
Date de intrare
Fişierul de intrare turnuri5.in conţine pe prima linie trei numere naturale N M şi T care reprezintă, N - numărul de linii, M - numărul de coloane şi T - numărul de turnuri.
Pe următoarele T linii se află turnurile. Pe linia i se găsesc trei numere naturale hi, li şi ri care reprezintă hi - înălţimea turnului, li - capătul stâng al intervalului turnului pe coloane, ri - capătul drept al intervalului turnului pe coloane.
Date de ieşire
Fişierul de ieşire turnuri5.out trebuie să conţină o linie. Pe aceea linie se afla un număr natural D care reprezintă numărul de dreptunghiuri valide pe care le poate desena modulo 109 + 7.
Restricţii
- 2 ≤ N, M ≤ 109
- 0 ≤ T ≤ 100 000
- 0 ≤ hi ≤ N - 1, 0 ≤ li < ri ≤ M - 1
- Două dreptunghiuri sunt diferite dacă colţul stânga sus sau colţul dreapta jos diferă.
- Pentru teste în valoare de 5 puncte, se garantează N, M, T ≤ 10
- Pentru teste în valoare de 10 puncte, se garantează N, M ≤ 50, T ≤ 10
- Pentru teste în valoare de 20 puncte, se garantează N, M ≤ 100
- Pentru teste în valoare de 30 puncte, se garantează N, M ≤ 1 000
- Pentru teste în valoare de 50 puncte, se garantează N, T ≤ 1 000, M ≤ 109
- Problema va fi evaluată pe teste în valoare de 90 de puncte.
- Exemplele vor reprezenta teste în valoare de 10 puncte "din oficiu".
Exemplu
| turnuri5.in | turnuri5.out |
|---|---|
| 5 6 1 2 2 3 | 33 |
| 10 12 3 5 1 4 1 7 9 8 10 11 | 507 |
