Fişierul intrare/ieşire:	trasee.in, trasee.out	Sursă	Lot Botosani 2012 - Baraj 3 Seniori
Autor	Zoltan Szabo	Adăugată de	Adrian Budau •freak93
Timp execuţie pe test	0.05 sec	Limită de memorie	20480 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Trasee

Transportul local în oraşul ISANOTOB este rezolvat optim cu ajutorul microbuzelor. Traseele au fost concepute în aşa fel încât două microbuze să nu aibă nicio porţiune comună de drum, în afară de intersecţii. Orice traseu poate fi reprezentat ca un segment sau o linie frântă formată din mai multe segmente perpendiculare. Linia frântă poate fi deschisă sau închisă.
Traseele sunt memorate pe o hartă dreptunghiulară formată din n x m pătrate identice. Aceste pătrate le vom nota cu a_ij (1≤i≤n,1≤j≤m). Vom atribui hărţii şi un sistem de coordonate cu n x m puncte, cu axele de coordonate Ox orientată spre dreapta, şi axa Oy orientată în jos. La intersecţia axelor se găseşte punctul de coordonate (0, 0), astfel colţul dreapta-jos al fiecărui pătrat a_ij are coordonatele (i, j) 1≤i≤n şi 1≤j≤m.
Două trasee se pot intersecta, dar nu pot avea niciun segment comun.
În figura 1, pe o hartă de dimensiuni 4 × 3, vedem patru trasee:
1. Primul traseu, desenat cu linie dublă, are pornirea din punctul de coordonate (1,2), şi sosirea în punctul de coordonate (1,2), Adică este un traseu închis (ciclu). La fel de corect ar fi dacă punctul de pornire ar fi punctul (2,2) şi oprirea (2,2), harta nu s-ar schimba.
2. Traseul al doilea, desenat cu linie triplă porneşte din punctul de coordonate (3,1) şi se termină în punctul de coordonate (3,3).
3. Traseul al treilea, desenat cu linie punctată, are ca puncte de pornire, respectiv de sosire, punctele de coordonate (4,1) respectiv (2,2).
4. Traseul al patrulea, desenat cu linie întreruptă, are ca puncte de pornire, respectiv de sosire, punctele de coordonate (4,1) respectiv (2,2).

În continuare ne vor interesa segmentele de pe hartă, fără să ştim cărui traseu îi aparţin. De aceea vom desena toate traseele cu linie îngroşată. Această hartă este memorată ca o matrice de dimensiuni n x m şi o vom numi matricea traseelor, în care fiecare element a_i,j este egal cu numărul de segmente ce fac parte din vreun traseu, deci valorile posibile pot fi 0,1,2,3 sau 4. Matricea traseelor din figura 2 corespunde hărţii traseelor din figura 1.
Matricea-hartă de dimensiuni 3n x 3m este o altă metodă de afişare a hărţii traseelor, în care orice nod de coordonate (i,j) va fi înlocuit cu o matrice-nod de dimensiuni 3 × 3. Orice element matrice-nod poate avea 16 valori distincte în funcţie de legăturile existente spre Nord, Sud, Est sau Vest:

Matricea-hartă din figura 3 corespunde hărţii traseelor din figura 1.

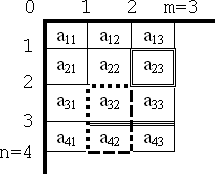
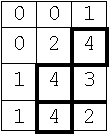
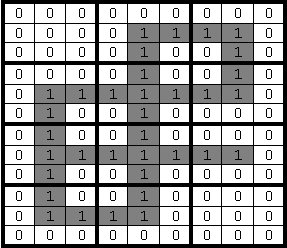
                 figura 1                                   figura 2                                          figura 3
              harta traseelor                   matricea traseelor                              matricea-hartă

Cerinţă

Cunoscând matricea traseelor şi toate punctele de pornire şi de sosire ale traseelor, se cere matricea-hartă corespunzătoare.

Date de intrare

Fişierul de intrare trasee.in conţine pe prima linie numerele n m k separate prin spaţiu, n şi m cu semnificaţiile din enunţ, iar k, numărul traseelor de pe hartă. Următoarele n linii conţin câte m numere separate prin spaţiu, reprezentând matricea traseelor. Următoarele k linii conţin câte patru numere naturale x y u v separate cu câte un spaţiu, reprezentând pe harta traseelor, coordonatele punctelor de pornire şi sosire ale celor k trasee, (x,y) respectiv (u,v).

Date de ieşire

Fişierul de ieşire trasee.out va conţine 3n linii cu câte 3m cifre 0 sau 1 neseparate prin spaţii, reprezentând matricea-hartă corespunzătoare hărţii traseului.

Restricţii şi precizări

• 3 ≤ m,n ≤ 500
• 1 ≤ k ≤ 350 000
• se acceptă orice soluţie corectă
• fiecare traseu are cel puţin un segment, fiecare segment aparţine unui singur traseu
• pentru 25% din teste m,n < 10
• pentru alte 25% din teste m,n < 40

Exemplu

Cum se trimit solutii?