Fişierul intrare/ieşire:	superpoligon.in, superpoligon.out	Sursă	Junior Challenge 2018
Autor	Alexandru Petrescu	Adăugată de	Junior Challenge •JuniorChallenge2018
Timp execuţie pe test	0.25 sec	Limită de memorie	524288 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Superpoligon

Anul trecut, Marcel era expert in figuri geometrice simple. Stia sa gaseasca pana si numarul de perechi de triunghiuri confundabile care se pot forma, alegand ca varfuri puncte dintr-un set dat. Mai nou, Marcel s-a şmeckerit si va propune sa rezolvati o generalizare:

Cerinta

Se dau N puncte distincte, un numar K si un numar M. Pentru fiecare r de la 3 la K, se cere numarul modulo M de perechi ordonate de poligoane confundabile de cate r puncte care se pot forma, alegand ca varfuri puncte dintr-un set dat. Fiecare poligon se poate auto-intersecta, dar nu poate poate contine acelasi punct de 2 ori.

Doua poligoane se considera confundabile daca exista o translatie astfel incat poligoanele sa se suprapuna perfect. De exemplu, orice poligon e confundabil cu el insusi. Atentie: Suprapunerea se face verifcand daca varfurile coincid, nu daca liniile coincid - fapt relevant in cazul punctelor coliniare: (0, 0) - (0, 1) - (0, 3) e diferit de (0, 0) - (0, 2) - (0, 3).

Doua poligoane sunt identice daca punctele unuia se obtin printr-o permutare circulara a altuia. De exemplu, (0, 0) - (0, 1) - (0, 2) e acelasi poligon cu (0, 1) - (0, 2) - (0, 0), dar e diferit de (0, 0) - (0, 2) - (0, 1).

Date de intrare

Fişierul de intrare superpoligon.in contine pe prima linie numerele naturale N, K si M (10⁸ ≤ M ≤ 10⁹ + 7) si pe urmatoarele N linii cate 2 numere intregi cu valoarea absoluta mai mica decat 10⁹ reprezentand coordonatele punctelor.

Date de ieşire

În fişierul de ieşire superpoligon.out se vor afla K - 2 linii, pe a i-a dintre ele fiind scris restul numarului cerut pentru r = i + 2 modulo M.

Subtaskuri

• Subtask 1 - 10 puncte: 3 ≤ K ≤ N ≤ 8, M = 10⁹ + 7
• Subtask 2 - 30 de puncte: 3 = K ≤ N ≤ 100, M = 10⁹ + 7
• Subtask 3 - 15 de puncte: 3 ≤ K ≤ N ≤ 40, M = 10⁹ + 7
• Subtask 4 - 15 de puncte: 3 ≤ K ≤ N ≤ 40
• Subtask 5 - 15 de puncte: 3 ≤ K ≤ N ≤ 1.000, M = 10⁹ + 7
• Subtask 6 - 15 de puncte: 3 ≤ K ≤ N ≤ 1.000

Exemplu

Explicaţie

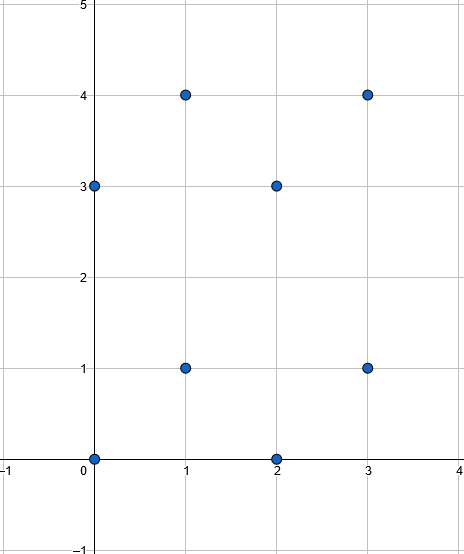
Exista 160 de perechi de triunghiuri confundabile, cum ar fi { (0, 0), (0, 2), (1, 1) } cu { (3, 0), (3, 2), (4, 1) }.
Observati ca { (0, 0), (0, 2), (1, 1) } si { (3, 0), (3, 2), (4, 1) } este considerata o perechie diferita de { (0, 0), (1, 1), (0, 2) } cu { (3, 0), (4, 1), (3, 2) }.
Remarcati ca { (0, 0), (0, 2), (1, 1) } si { (3, 0), (3, 2), (4, 1) } este considerata o pereche identica cu { (0, 2), (1, 1), (0, 0) } si { (3, 2), (4, 1), (3, 0) }.
De asemenea, { (0, 0), (0, 2), (1, 1) } si { (3, 0), (3, 2), (4, 1) } este considerata o pereche diferita de { (3, 0), (3, 2), (4, 1) } si { (0, 0), (0, 2), (1, 1) }

Cum se trimit solutii?