| Fişierul intrare/ieşire: | summax.in, summax.out | Sursă | OJI 2016, clasele 11-12 |
| Autor | Zoltan Szabo | Adăugată de | |
| Timp execuţie pe test | 0.75 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate |
Vezi solutiile trimise | Statistici
Sum Max
Avem o matrice triunghiulară cu N linii, cu elemente numere întregi. În această matrice putem construi un traseu după următoarea regulă:
- primul element al traseului este a1,1
- dacă elementul ai,j aparţine traseului, atunci următorul element al traseului poate fi doar ai+1,j sau ai+1,j+1, pentru orice 1 ≤ j ≤ i < N.
Traseul se va codifica cu numerele de ordine ale coloanelor, parcurgând liniile de la 1 la N. Valoarea traseului este egală cu suma elementelor ce îl formează.
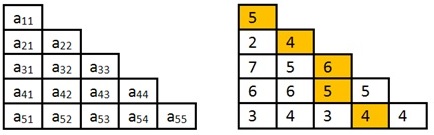
Traseul evidenţiat în exemplul de mai sus are valoarea 5+4+6+5+4=24, şi se codifică cu 1 2 3 3 4.
Fie mulţimea tuturor traseelor de valoare maximă generate în ordine lexicografică şi numerotate. Pentru exemplul de mai sus avem şase trasee de lungime maximă:
- traseul 1: 1 1 1 1 2 (5+2+7+6+4=24)
- traseul 2: 1 1 1 2 2 (5+2+7+6+4=24)
- traseul 3: 1 2 2 2 2 (5+4+5+6+4=24)
- traseul 4: 1 2 3 3 4 (5+4+6+5+4=24)
- traseul 5: 1 2 3 4 4 (5+4+6+5+4=24)
- traseul 6: 1 2 3 4 5 (5+4+6+5+4=24)
Cerinţă
Cunoscând dimensiunile şi elementele unei matrice triunghiulare, respectiv două numere naturale st şi dr, se cere să se determine:
- Numărul total al traseelor de valoare maximă. În cazul în care această valoare depaşeşte 2 000 000 000, se va tipări valoarea 2 000 000 001 (fără spaţii).
- Traseele cu numerele de ordine st, st+1, ... , dr.
Date de intrare
Fişierul summax.in conţine pe prima linie un număr natural v. Pentru toate testele de intrare, numărul v poate avea doar valoarea 1 sau valoarea 2. A doua linie conţine trei numere naturale N, st şi dr, separate prin spaţiu. Următoarele N linii conţin câte o linie a matricei triunghiulare astfel: linia i conţine i elemente, şi anume valorile ai,1 ai,2 ... ai,i pentru orice 1 ≤ i ≤ N.
Date de ieşire
Dacă valoarea lui v este 1, se va rezolva numai punctul 1 din cerinţă.
În acest caz, în fişierul de ieşire summax.out se va scrie un singur număr natural ce reprezintă numărul traseelor de lungime maximă.
Dacă valoarea lui v este 2, se va rezolva numai punctul 2 din cerinţă.
În acest caz, în fişierul de ieşire summax.out se vor tipări pe câte o linie N numere naturale separate prin spaţiu, reprezentând codificările traseelor de valoare maximă cu numerele de ordine st, st+1, ... , dr.
Restricţii
- 1 ≤ N ≤ 2 000
- 1 ≤ st ≤ dr ≤ 2 000 000 000
- 1 ≤ dr - st ≤ 1 000
- Elementele matricei triunghiulare sunt numere naturale strict pozitive.
- Valoarea maximă a traseului nu depăşeşte 1 000 000 000.
Exemplu
| summax.in | summax.out |
|---|---|
| 1 5 2 4 5 2 4 7 5 6 6 6 5 5 3 4 3 4 4 | 6 |
| 2 5 2 4 5 2 4 7 5 6 6 6 5 5 3 4 3 4 4 | 1 1 1 2 2 1 2 2 2 2 1 2 3 3 4 |
Explicaţie
În primul exemplu valoarea lui v este 1, deci se rezolvă doar cerinţa 1. Numărul traseelor de valoare maximă este 6.
În al doilea exemplu valoarea lui v este 2, deci se rezolvă doar cerinţa 2. Se tipăresc codificările traseelor cu numerele de ordine 2, 3 şi 4.


