Pagini recente » Istoria paginii problema/infasuratoare | Diferente pentru problema/infasuratoare intre reviziile 50 si 80 | Statistici Oprea Mihai Adrian (Mihai145) | Ciclu Eulerian | Numerele lui Stirling

Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2010-05-29 11:43:11.
Revizia anterioară Revizia următoare

Fişierul intrare/ieşire:	stirling.in, stirling.out	Sursă	Arhiva Educationala
Autor	Arhiva Educationala	Adăugată de	Matei-Dan Epure •motty
Timp execuţie pe test	0.075 sec	Limită de memorie	20480 kbytes
Scorul tău	N/A	Dificultate	N/A

Numerele lui Stirling

Se definesc numerele lui Stirling de speţa I, s(n,m), ca fiind numărul de permutări de ordin n cu exact m cicluri. Similar, se definesc numerele lui Stirling de speţa a II-a, S(n,m), ca fiind numărul de partiţionări ale unei mulţimi de n elemente în m submulţimi nevide.

Cerinţă

Pentru n şi m date, să se calculeze una dintre cele 2 funcţii, s(n,m) sau S(n,m).

Date de intrare

Prima linie a fişierului de intrare stirling.in conţine T, numărul de teste. Fiecare din următoarele T linii conţine câte un set de 3 numere naturale separate prin câte un spaţiu, x, n şi m. Variabila x poate lua valorile 1 sau 2. Dacă x este 1 se doreşte determinarea lui s(n,m), iar dacă x este 2 se doreşte determinarea lui S(n,m).

Date de ieşire

Fişierul stirling.out conţine exact T linii, câte una pentru fiecare test din fişierul de intrare. Linia a i-a conţine rezultatul, modulo 98999, pentru testul i.

Restrictii

1 ≤ T ≤ 1000
0 ≤ N, M ≤ 200

Exemplu

stirling.in	stirling.out
3 1 1 1 1 3 2 2 1 1	1 -3 1

Indicaţii de rezolvare

Ideea "naivă" de rezolvare a acestei probleme este determinarea răspunsului generând efectiv, prin metoda backtracking, fie toate permutările de ordin n şi determinarea celor care au m cicluri, fie toate partiţionările unei mulţimi de n elemente în m submulţimi nevide. Această rezolvare are complexitate exponenţială şi va obţine 10 puncte.

În urma unor demonstraţii matematice (explicate pe larg în link-urile de mai jos), pentru funcţiile lui Stirling se pot obţine recurenţele:
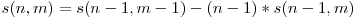$s(n,m) = s(n-1,m-1) - (n-1)*s(n-1,m)$ şi $S(n,m) = S(n-1,m-1) + m*S(n-1,m)$ .

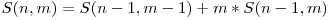O primă metodă de rezolvare ce foloseşte observaţia de mai sus este determinarea valorilor s(n,m) sau S(n,m), implementând un algoritm recursiv ce modelează relaţiile de recurenţă prezentate. Această metodă obţine 50 de puncte. O sursă pe această idee se găseşte aici.

Soluţia optimă pentru problema de faţă se bazează pe preprocesarea valorilor s(n,m) şi S(n,m), implemenând de asemenea relaţiile de recurenţă prezentate. Astfel, se va putea răspunde la fiecare test în timp O(1), complexitatea totala fiind O(N*M + T). Această rezolvare obţine 100 de puncte. O sursa pe această idee se găseşte aici.