Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | ssnd.in, ssnd.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de | |
| Timp execuţie pe test | 0.05 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Suma si numarul divizorilor
Divizorii unui număr natural n reprezintă mulţimea de numere naturale, mai mici sau egale cu n, cu proprietatea că divid pe n. Să se determine pentru t numere naturale cardinalul acestei mulţimi şi restul împărţirii sumei elementelor mulţimii la 9973.
Date de intrare
Fişierul de intrare ssnd.in conţine pe prima linie un număr natural t. Pe următoarele t linii se va afla câte un număr natural n.
Date de ieşire
În fişierul de ieşire ssnd.out se vor afla t linii, fiecare linie conţinând 2 numere naturale, reprezentând răspunsul pentru fiecare din cele t întrebări.
Restricţii
- 1 ≤ t ≤ 10
- 1 ≤ n ≤ 1012
Exemplu
| ssnd.in | ssnd.out |
|---|---|
| 3 8 12 13 | 4 15 6 28 2 14 |
Explicaţie
Pentru 8, divizorii lui 1, 2, 4, 8, iar suma lor este 1+2+4+8 = 15.
Divizorii lui 12 sunt 1, 2, 3, 4, 6, 12, iar suma lor este 1+2+3+4+6+12 = 28.
13 este număr prim, prin urmare are doar 2 divizori, pe 1 şi pe el însuşi, iar suma lor este 14.
Indicaţii de rezolvare
O soluţie brută, care parcurge toate numerele de la 1 la n şi numără toţi divizorii ar trebui să obţină aproximativ 30 de puncte.
Din descompunerea numărului în factori primi se pot calcula atât suma, cât şi numărul de divizori astfel: dacă 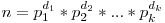 , atunci numărul de divizori este egal cu
, atunci numărul de divizori este egal cu 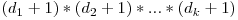 , iar suma lor
, iar suma lor 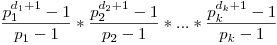
 Poti vedea testele pentru aceasta problema accesand
Poti vedea testele pentru aceasta problema accesand 