Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | smin.in, smin.out | Sursă | Lot Juniori 2009 - Baraj 4 |
| Autor | Suzana Galatan | Adăugată de |  Cezar Mocan •CezarMocan |
| Timp execuţie pe test | 0.4 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Smin
Ana are un joc nou. Pe o tablă pătrată este trasat un grid format din celule pătratice de dimensiune 1. În oricare dintre colţurile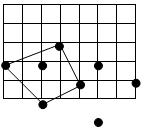 
oricarei celule, Ana poate înfige câte un beţişor perpendicular pe tablă. După ce a plasat n beţişoare, Ana ia dintr-o cutie (cu un număr suficient de mare de corzi elastice circulare) câte o coardă cu care înconjoară trei sau mai multe beţişoare. Fiecare coardă este bine întinsă şi formează pe tablă un contur poligonal.
În figura alăturată este folosită o coardă ce formează un contur poligonal cu 4 laturi cu care sunt înconjurate 5 dintre cele 8 beţişoare de pe tablă.
Jocul se încheie când au fost plasate atâtea coarde încât toate beţişoarele de pe tablă să se afle pe marginea sau în interiorul a cel puţin unul dintre contururile poligonale formate. Scopul jocului este ca amplasarea corzilor să fie făcută convenabil astfel încât totalul ariilor contururilor poligonale formate să fie minim.
Cerinţă
Cunoscând coordonatele celor n beţişoare (x1, y1), (x2, y2), …, (xn, yn) măsurate faţă de unul dintre colţurile gridului, Ana doreşte să găsească suma minimă a ariilor poligonale obţinute prin amplasarea convenabilă a coardelor, astfel încât fiecare beţişor să se găsească în interiorul sau pe conturul a cel puţin un astfel de poligon.
Date de intrare
În fişierul smin.in pe prima linie se găseşte numărul natural n. Pe fiecare dintre următoarele n linii, se află câte două numere naturale: x y.
Date de ieşire
În fişierul smin.out se va scrie numărul real s, reprezentând suma minimă a ariilor poligoanelor convexe care acoperă toate punctele date.
Restricţii
- 3 ≤ N ≤ 17
- 0 ≤ x, y ≤ 100
- Datele de intrare nu vor conţine trei beţişoare plasate în puncte coliniare din planul tablei
- Suma cerută se obţine însumând ariile tuturor poligoanelor, indiferent dacă unele poligoane se suprapun sau nu
- Modulul diferenţei dintre valoarea reală a lui s şi cea afişată este mai mic decât 0.001
Exemplu
| smin.in | smin.out |
|---|---|
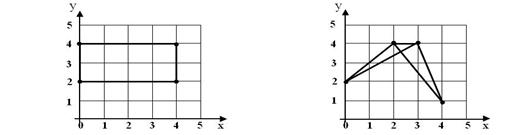
| 4 0 2 0 4 4 4 4 2 | 8.000 |
| 4 0 2 2 4 3 4 4 1 | 2.5000 |
Explicaţie
In primul exemplu aria minimă este dreptunghiul din prima figură, cu cele patru beţişoare în vârfuri. Se foloseşte o singură coardă elastică. In cel de-al doilea aria minimă este suma ariilor celor două triunghiuri delimitate de două corzi elastice din a doua figură.
