Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | sireturi.in, sireturi.out | Sursă | ONIS 2014, Runda 2 |
| Autor | Stefan Ciobaca | Adăugată de | |
| Timp execuţie pe test | 0.5 sec | Limită de memorie | 65536 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Sireturi
Gigel e fascinat atât de şireturi (de la pantofi) cât şi de divizori.
De exemplu, ieri a văzut două moduri interesante de a lega şireturile la pantofii cu 6 perechi de găuri:
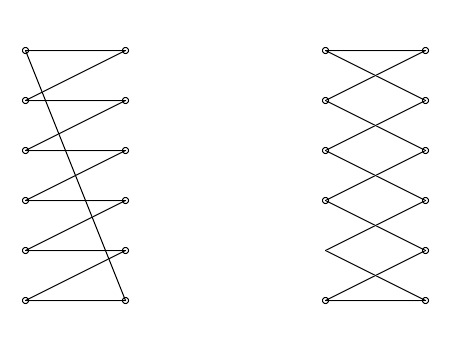
Imediat s-a întrebat în câte moduri pot fi legate şireturile la pantofii cu n perechi de găuri. De exemplu, pentru 3 perechi de găuri, Gigel şi-a dat seama că sunt 4 posibilităţi:
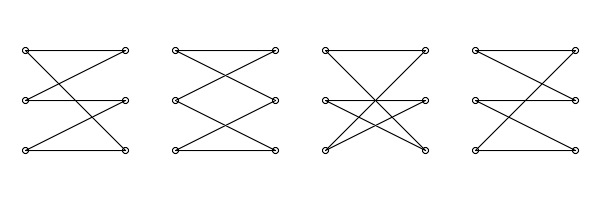
Ce legatură au pantofii cu divizorii? Fiind mai sadic, Gigel nu e interesat să ştie exact numărul de posibilităţi de a lega şireturile -- e mult mai interesat să ştie câţi divizori naturali are numărul de posibilităţi de a lega şireturile pentru pantofi cu n perechi de găuri. Scrieţi un program care să-l ajute.
Date de intrare
Fişierul de intrare sireturi.in conţine pe prima linie numărul de teste T. Pe următoarele T linii se găseşte un număr n reprezentând numărul de găuri de la pantofi.
Date de ieşire
În fişierul de ieşire sireturi.out afişaţi pe câte o linie pentru fiecare test numărul de divizori naturali ale numărului de posibilităţi de a lega şireturile la pantofii cu n găuri. Rezultatul trebuie afişat modulo 9901.
Restricţii
- pentru a lega şireturile, prin fiecare gaură trebuie trecut şiretul o singură dată (şiretul se introduce întotdeauna de deasupra spre dedesubt)
- de la o gaură, şiretul trebuie să meargă la o gaură în cealaltă parte a pantofului
- două tipuri de a lega şiretul nu se consideră diferite dacă diferă doar prin faptul că un segment trece pe deasupra sau pe dedesubtul altui segment de şiret
- evident, când legăm şireturile, perechea de găuri cea mai de sus trebuie legata direct (acolo se face funda ;-) )
- 1 ≤ n ≤ 7500
- 1 ≤ T ≤ 10000
Exemplu
| sireturi.in | sireturi.out |
|---|---|
| 2 2 3 | 1 3 |
Explicaţie
Pentru pantofi cu două perechi de găuri, există o singură modalitate de a lega şireturile. Numărul 1 are exact un divizor natural; modulo 9901 obţinem 1.
Pentru pantofi cu trei perechi de găuri, există 4 modalităţi de a lega şireturile (după cum s-a vazut mai sus). Numărul 4 are exact 3 divizori: 1, 2, 4. Restul impartirii lui 3 la 9901 e chiar 3.
