| Fişierul intrare/ieşire: | simetric.in, simetric.out | Sursă | ONI 2010, clasa a 9-a |
| Autor | Filip Cristian Buruiana | Adăugată de | |
| Timp execuţie pe test | 0.1 sec | Limită de memorie | 6144 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Simetric
O matrice pătratică A care are P linii şi P coloane este simetrică dacă şi numai dacă pentru orice indici i şi j între 1 şi P avem că Ai,j = Aj,i. Astfel, matricea din figura 1 este simetrică, iar cea din figura 2 nu este, deoarece există cel puţin o pereche de indici (de exemplu i = 2 şi j = 3), pentru care Ai,j este diferit de Aj,i.
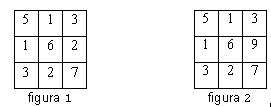
Pentru o matrice dată cu M linii şi N coloane, definim submatricea de vârfuri (l1, c1) şi (l2, c2), cu 1 ≤ l1 ≤ l2 ≤ M şi 1 ≤ c1 ≤ c2 ≤ N, ca fiind tabloul format din toate elementele de coordonate i şi j astfel încât l1 ≤ i ≤ l2 şi c1 ≤ j ≤ c2.
Cerinţă
Se dă o matrice cu M linii şi N coloane în care toate elementele sunt numere naturale. Fie L latura maximă a unei submatrici simetrice din această matrice. Pentru fiecare dimensiune i între 1 si L să se determine câte submatrici simetrice şi cu latura i ale matricii date există.
Date de intrare
Prima linie a fişierului simetric.in conţine numerele M şi N, separate de exact un spaţiu, reprezentând numărul de linii, şi respectiv de coloane, ale matricii care se citeşte. Fiecare din următoarele M linii conţine câte N numere naturale, despărţite de exact un spaţiu, reprezentând elementele matricii.
Date de ieşire
Fişierul de ieşire simetric.out conţine exact L linii, unde L este latura maximă a unei submatrici simetrice din matricea considerată. Linia i conţine numărul de submatrici simetrice de latură i.
Restricţii şi precizări
- 2 ≤ M, N ≤ 400.
- Elementele matricii sunt numere naturale cuprinse între 1 şi 30000.
Exemplu
| simetric.in | simetric.out |
|---|---|
| 4 5 5 1 3 6 9 1 6 2 8 9 3 2 7 5 1 9 8 5 3 8 | 20 3 2 |
Explicaţie
Există 20 de submatrici simetrice de latură 1 (fiecare celulă este considerată submatrice), 3 submatrici simetrice de latură 2 şi 2 de latură 3. Submatricile simetrice de latură 3 sunt:
5 1 3 6 2 8
1 6 2 2 7 5
3 2 7 8 5 3
