Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | sdo.in, sdo.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de | |
| Timp execuţie pe test | 0.6 sec | Limită de memorie | 36864 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Statistici de ordine
Se dă o mulţime de numere naturale A, de N elemente şi un număr natural K. Să se determine a K-a statistică de ordine (al K-lea cel mai mic element) a mulţimii.
Date de intrare
Fişierul de intrare sdo.in conţine pe prima linie N şi K, iar pe a doua linie N numere naturale, reprezentând elementele mulţimii.
Date de ieşire
În fişierul de ieşire sdo.out se va afla un singur număr natural, reprezentând a K-a statistică de ordine a mulţimii.
Restricţii
- 1 ≤ K ≤ N ≤ 3 000 000
- Toate cele N numere sunt din intervalul [1, 109]
Exemplu
| sdo.in | sdo.out |
|---|---|
| 8 3 1 10 4 13 7 6 11 14 | 6 |
Explicaţie
În exemplu, se observă că elementele aranjate în ordine crescătoare sunt: 1 4 6 7 10 11 13 14, prin urmare al 3-lea cel mai mic element este 6.
O primă soluţie(?), care numără pentru fiecare element câte elemente sunt mai mici decât el, se găseşte aici, şi ar trebui să obţină ... puncte.
Altă soluţie(?) care sortează elementele în ordine crescătoare şi are complexitatea 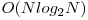 ar trebui să obţină ... puncte.
ar trebui să obţină ... puncte.
O altă soluţie(?), cu complexitatea 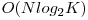 , care foloseşte un heap pentru a menţine cele mai mici K elemente ar trebui să obţină ... puncte.
, care foloseşte un heap pentru a menţine cele mai mici K elemente ar trebui să obţină ... puncte.
În final, soluţia(?) care ar trebui să obţină 100 de puncte foloseşte funcţia de partiţionare a quicksort-ului pentru a determina a K-a statistică de ordine. Practic, acest algoritm este foarte asemănător quicksort-ului, doar că în loc să se sorteze tot şirul se vor sorta doar anumite porţiuni care ajută la determinarea soluţiei. Acest algoritm este implementat şi în STL, funcţia nth_element găsindu-se în headerul algorithm. O sursă demonstrativă se găseşte aici(?). Complexitatea acestui algoritm este în medie 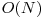 , în cel mai defavorabil caz putând atinge
, în cel mai defavorabil caz putând atinge 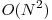
 Poti vedea testele pentru aceasta problema accesand
Poti vedea testele pentru aceasta problema accesand 