Pagini recente » Diferente pentru problema/cmap intre reviziile 24 si 32 | Diferente pentru problema/cmap intre reviziile 13 si 32 | Diferente pentru problema/cmap intre reviziile 16 si 32 | Diferente pentru problema/cmap intre reviziile 26 si 32 | Radix Sort

Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2014-01-25 21:48:59.
Revizia anterioară Revizia următoare

Fişierul intrare/ieşire:	radixsort.in, radixsort.out	Sursă	Arhiva Educationala
Autor	Arhiva Educationala	Adăugată de	Laurentiu Ion •laurion
Timp execuţie pe test	0.75 sec	Limită de memorie	131072 kbytes
Scorul tău	N/A	Dificultate	N/A

Radix Sort

Se dau N numere naturale, intr-o ordine oarecare, si se cere sortarea lor in ordine crescatoare.

Date de intrare

Fişierul de intrare radixsort.in va avea pe prima linie numerele N, A, B si C separate prin cate un spatiu.
Cele N numere se vor genera dupa urmatoarea formula:
v[i] = B, pentru i = 1
v[i] = (A * v[i-1] + B) % C, pentru 2 ≤ i ≤ N

Date de ieşire

În fişierul de ieşire radixsort.out se vor tipari pe prima linie numerele generate de pe pozitiile 1, 11, 21, 31, ... (din 10 in 10) in ordine crescatoare, separate printr-un singur spatiu.

Restricţii

1 ≤ N ≤ 10 000 000
Toate cele N numere vor fi cuprinse intre 0 si 2³¹-1 inclusiv.

Exemplu

radixsort.in	radixsort.out
100 12 38 123	2 14 23 38 50 59 71 80 98 110

Indicatii de rezolvare

Structura problemei cere implementarea algoritmului de sortare Radix Sort, fiindca numerele sunt naturale.

Complexitatea lui este 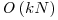$\mathit{O} \left( kN \right)$ , unde k este lungimea medie a numerelor sau 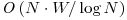$\mathit{O} \left( N \cdot W/\log N \right)$ , unde W este marimea in biti a word-ului calculatorului (32 pentru int; explicatia aici).

Acest algoritm nu se bazeaza pe comparatii deci nu este restrictionat de limita 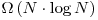$\Omega \left( N \cdot \log N \right)$ precum Merge Sort sau Quick Sort

O solutie bazata pe comparatii, folosind functia std::sort() obtine aproximativ 30 de puncte.

O sursa de 100 de puncte se gaseste aici. Aceasta solutie se bazeaza pe Counting Sort, care are complexitatea 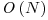$\mathit{O} \left( N \right)$ dar este limitat de faptul ca foloseste memorie suplimentara egala cu maximul dintre numere, care poate ajunge la 2³¹-1 in acest caz. Astfel impartim numerele in 4 bucket-uri de cate un byte (pe care le numim "cifre") si le sortam incepand cu cea mai putin semnificativa.