Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | pinex.in, pinex.out | Sursă | Arhiva Educationala |
| Autor | Arhiva Educationala | Adăugată de | |
| Timp execuţie pe test | 1 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Principiul includerii si excluderii
A gamă foarte largă de probleme în cadrul concursurilor de informatică şi nu numai se rezolvă folosind principiul includerii şi excluderii. Deşi teoria poate părea greu de înţeles, mă voi strădui să ofer o explicaţie cât mai clară pentru cei interesaţi.
Principiul enunţă faptul că fiind date N multimi finite A1,A2,A3...An, relaţia de mai jos este adevărată.
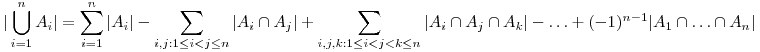
Pentru demonstraţie, vom pleca de la cazul banal când avem doar două mulţimi, fie acestea A şi B. Dacă sunt disjuncte, este clar că reuniunea lor se calculează după relaţia 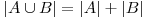 . Ne rămâne de rezolvat cazul când A şi B au cel puţin un element în comun. Relaţia anterioară numără elementele comune din cadrul reuniunii de două ori(o dată pentru A şi o dată pentru B), de aici apare nevoia să scădem numărul acestora din rezultat. Acest lucru este uşor de făcut, dat fiind faptul că pentru A şi B, numărul de elemente comune celor doua mulţimi este
. Ne rămâne de rezolvat cazul când A şi B au cel puţin un element în comun. Relaţia anterioară numără elementele comune din cadrul reuniunii de două ori(o dată pentru A şi o dată pentru B), de aici apare nevoia să scădem numărul acestora din rezultat. Acest lucru este uşor de făcut, dat fiind faptul că pentru A şi B, numărul de elemente comune celor doua mulţimi este 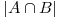 . Rezultă
. Rezultă 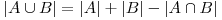 .
.
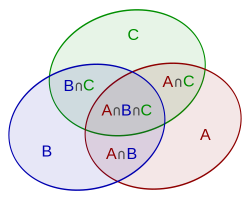
În diagrama din dreapta este reprezentat cazul cu trei muţimi A, B şi C. Relaţia de mai sus se extinde la 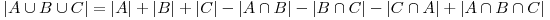 .
.
Pentru cazul general, având N mulţimi A1,A2,A3...An, vom presupune că există un element x din
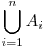 comun pentru exact k multimi, fie acestea Ai1,Ai2,Ai3...Aik. Vom considera cardinalele mulţimilor doar faţă de acest număr x (cu alte cuvinte, ignormăm celelalte elemente). Dacă vom face intersecţia a mai mult de k mulţimi, sau a unor mulţimi cu indicele de ordine diferit de i1,i2...ik, această intersecţie va fi evident vidă. Numărul de intersecţii a două mulţimi din cele k este C(k,2), numărul de intersecţii a trei mulţimi este C(k,3), etc. Cum am spus ca vom urmări doar elementul x, avem relaţia
comun pentru exact k multimi, fie acestea Ai1,Ai2,Ai3...Aik. Vom considera cardinalele mulţimilor doar faţă de acest număr x (cu alte cuvinte, ignormăm celelalte elemente). Dacă vom face intersecţia a mai mult de k mulţimi, sau a unor mulţimi cu indicele de ordine diferit de i1,i2...ik, această intersecţie va fi evident vidă. Numărul de intersecţii a două mulţimi din cele k este C(k,2), numărul de intersecţii a trei mulţimi este C(k,3), etc. Cum am spus ca vom urmări doar elementul x, avem relaţia 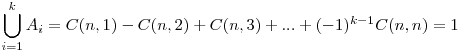 Rezultă relaţia de demonstrat este adevărată.
Rezultă relaţia de demonstrat este adevărată.
Pentru o demonstratie mai riguroasă puteţi citi de pe wikipedia sau de pe cut-the-knot.
Aplicaţie la teoria prezentă mai sus
Răspundeţi la M întrebări de tipul: „dându-se două numere naturale A şi B, să se determine numărul de numere mai mici ca A şi prime cu B ”. Două numere naturale (x,y) sunt prime între daca cmmdc(x,y)=1.
Care-i legătura?
În loc să calculăm în mod direct numărul de numere mai mici ca A şi prime cu B, ne va fi mai uşor să calculam numărul de numere mai mici ca A neprime cu B, şi apoi să scadem acest rezultat din A. Pentru aceasta, vom lua în considerare divizorii primi ai lui A, fie aceştia D1,D2...Dk. Este evident ca orice număr natural x care are cmmdc(x,A)≠1 va fi divizibil cu unul din numerele D1,D2...Dk. De aici rezultă că o sa avem k mulţimi formate din numerele naturale mai mici ca A şi prime cu câte unul din divizorii primi ai lui B - valoarea căutată este reprezentată de cardinalul reuniunii lor. Calcularea acestui cardinal implică principiul includerii şi exlcuderii. Pentru mai multe detalii citiţi indicaţiile de rezolvare.
Date de intrare
Fişierul de intrare pinex.in va conţine pe prima linie numărul M, reprezentând numărul de query-uri. Următoarele M linii vor conţine câte două numere A si B, cu semnificaţia din enunţ.
Date de ieşire
Fişierul de ieşire pinex.out va conţine M linii, pe linia i fiind răspunsul la a i-a întrebare.
Restricţii
- 1 ≤ M ≤ 500
- 1 ≤ A ≤ 1018
- 1 ≤ B ≤ 1012
- Pentru 30% din teste M ≤ 100, A,B ≤ 1 000
- Pentru 70% din teste A,B ≤ 109
Exemplu
| pinex.in | pinex.out |
|---|---|
| 3 10 5 20 6 50 30 | 8 7 14 |
Indicaţii de rezolvare
Vom calcula numărul de numere mai mici ca A neprime cu B. Fie D1,D2...Dk divizorii primi ai lui B. Fiecare astfel de divizor va determina o mulţime de numere 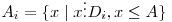 . Astfel, solţia va fi
. Astfel, solţia va fi 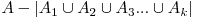 . Ştiind cardinalul fiecărei configuraţii de intersecţie între cele k mulţimi, vom putea folosi principiul includerii si excluderii pentru calcularea numărului căutat.
. Ştiind cardinalul fiecărei configuraţii de intersecţie între cele k mulţimi, vom putea folosi principiul includerii si excluderii pentru calcularea numărului căutat.
Să exemplificăm pentru A=50 şi B=30. Divizorii primi ai lui B sunt 2,3 şi 5, rezultă mulţimile 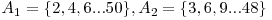 şi
şi 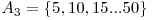 . Tabelul de mai jos ilustrează toate cele 7 mulţimi care vor apărea în operaţiile efectuate de noi, precum şi elementele conţinute de acestea.
. Tabelul de mai jos ilustrează toate cele 7 mulţimi care vor apărea în operaţiile efectuate de noi, precum şi elementele conţinute de acestea.
Aplicăm relaţia pentru trei mulţimi 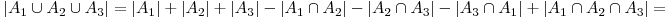
![= [50/2] + [50/3] + [50/5] - [50/6] - [50/15] - [50/10] + [50/30] = = [50/2] + [50/3] + [50/5] - [50/6] - [50/15] - [50/10] + [50/30] =](http://www.infoarena.ro/static/images/latex/ddfa457cc01ccf44a54723c48f53dd02_3.5pt.gif)
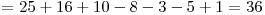
Soluţia în acest caz va fi 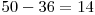 , cele 14 numere fiind
, cele 14 numere fiind 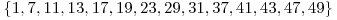
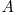 | 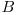 | 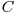 | 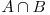 |  |  |  | |
 | |||||||
 |  | ||||||
 |  | ||||||
 |  | ||||||
 |  | ||||||
 |  |  |  | ||||
 | |||||||
 |  | ||||||
 |  | ||||||
 |  |  |  | ||||
 | |||||||
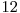 |  |  |  | ||||
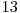 | |||||||
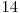 |  | ||||||
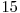 |  |  |  | ||||
 |  | ||||||
 | |||||||
 |  |  |  | ||||
 | |||||||
 |  |  |  | ||||
 |  | ||||||
 |  | ||||||
 | |||||||
 |  |  |  | ||||
 |  | ||||||
 |  | ||||||
 |  | ||||||
 |  | ||||||
 | |||||||
 |  |  |  |  |  |  |  |
 | |||||||
 |  | ||||||
 |  | ||||||
 |  | ||||||
 |  | ||||||
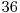 |  |  |  | ||||
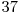 | |||||||
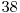 |  | ||||||
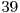 |  | ||||||
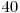 |  |  |  | ||||
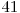 | |||||||
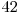 |  |  |  | ||||
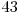 | |||||||
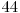 |  | ||||||
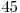 |  |  |  | ||||
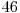 |  | ||||||
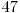 | |||||||
 |  |  |  | ||||
 | |||||||
 |  |  |  |
Detalii de implementare
Soluţia de 30 puncte presupune parcurgerea numerelor mai mici ca A la fiecare query, verificându-se primalitatea lor cu B. Această abordare are complexitate O(M*A*logB);
Pentru 70 puncte trebuie aplicat principiul includerii si excluderii descris mai sus. O sursă pe această idee puteţi găsi aici.
Optimizarea ce permite obţinerea punctajului maxim reprezintă precalcularea tutror numerelor prime mai mici ca 106. Astfel, atunci când determinăm divizorii primi ai lui B vom itera doar prin numere prime. Complexitatea acestei soluţii este O(M*logB*2NrDivB*NrDivB), unde prin NrDivB ne referim la numărul divizorilor primi ai lui B.
Aplicaţii
Reuniune
Suman
Mins
Pairs
Coin Changing Again, uva
Prime Frog, uva
Jap
Secventa farey
Cowfood
Rifleman sgu
Sweets, CEOI 2004
 Poti vedea testele pentru aceasta problema accesand
Poti vedea testele pentru aceasta problema accesand 