Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | perfect.in, perfect.out | Sursă | Lot 2006 Alba |
| Autor | Marinel Serban | Adăugată de | |
| Timp execuţie pe test | 0.025 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Perfect
Sa consideram secvente de grafuri neorientate de tipurile urmatoare:
Tipul A
Secventa grafurilor de tip A se construieste in modul ce se poate deduce din exemplele urmatoare:
A1 A2 A3 A4 A5

Observati ca graful An are 2n varfuri.
Tipul B
Secventa grafurilor de tip B se construieste dupa modelul urmator:
B1 B2 B3 B4
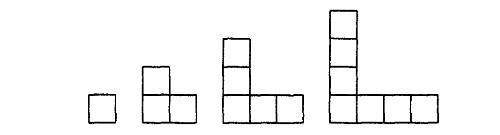
Tipul C
Secventa grafurilor de tip C se construieste dupa modelul urmator:
C1 C2 C3 C4
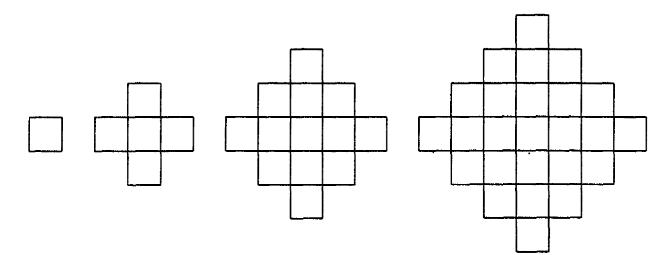
Se numeste cuplaj perfect in graf o modalitate de a alege muchii ale grafului astfel incat oricare varf din graf sa fie incident cu exact o muchie aleasa. Doua cuplaje sunt distincte daca exista o muchie care apartine unui cuplaj, dar nu apartine celuilalt.
Cerinta
Dat fiind un graf de unul dintre tipurile din enunt, sa se determine numarul de cuplaje perfecte distincte ale grafului respectiv.
Date de intrare
Fisierul de intrare perfect.in contine o singura linie pe care se afla un caracter si un numar natural nenul n, separate printr-un spatiu. Caracterul poate fi A, B sau C si indica tipul grafului. Numarul natural n indica numarul de ordine al grafului in secventa de grafuri de tipul specificat de caracter.
Date de iesire
Fisierul de iesire perfect.out va contine o singura linie pe care va fi scris numarul de cuplaje perfecte ale grafului din fisierul de intrare.
Restrictii
- 1 ≤ n ≤ 100
Exemplu
| perfect.in | perfect.out |
|---|---|
| A 4 | 5 |
| B 2 | 4 |
| C 2 | 8 |
Explicatie
Cele 5 cuplaje perfecte ale grafului A4 sunt:
img 1
Cele 4 cuplaje perfecte ale grafului B2 sunt:
img 2
Cele 8 cuplaje perfecte ale grafului C2 sunt:
img 3
