Fişierul intrare/ieşire:	penal.in, penal.out	Sursă	Stelele Informaticii 2006, clasele 9-10
Autor	Silviu-Ionut Ganceanu	Adăugată de	Bogdan-Cristian Tataroiu •bogdan2412
Timp execuţie pe test	0.075 sec	Limită de memorie	20096 kbytes
Scorul tău	N/A	Dificultate	2/5

Vezi solutiile trimise | Statistici

Problema penala

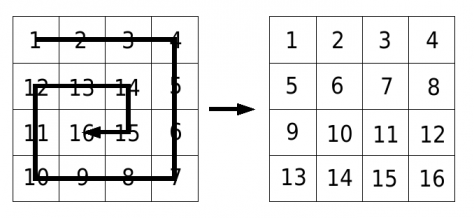Deoarece a mancat prea multe bomboane, Algorel a inceput sa se joace cu ele. El este in posesia a N² bomboane pe care le aseaza astfel incat ele formeaza o matrice de dimensiuni N x N. Dupa ce le-a asezat, el se uita mandru la ele si apoi incepe sa le schimbe asezarea in mod repetitiv. Se defineste o operatie ca fiind o reordonare a elementelor matricei dupa urmatoarea regula: mai intai stabileste o ordine a bomboanelor pornind din coltul stanga sus al matricii in forma de spirala; apoi le dispune, in ordinea stabilita, intr-o noua matrice completand prima linie de la stanga la dreapta, apoi a doua linie de la stanga la dreapta, s.a.m.d. (vezi desenul alaturat).

P dintre cele N² bomboane sunt mai speciale: contin alcool. Parintii lui Algorel stiu pozitia initiala a fiecarei bomboane speciale si cate operatii a efectuat acesta. Pentru a il supraveghea cat mai atent, ei vor sa stie pozitia fiecarei bomboane speciale dupa fiecare operatie efectuata de Algorel.

Date de intrare

Pe prima linie a fisierului penal.in se afla 3 numere naturale N M P - N reprezinta latura matricii de bomboane a lui Algorel, M reprezinta numarul de operatii efectuate de acesta si P reprezinta numarul de bomboane speciale. A doua linie a fisierului contine P perechi de numere naturale separate prin spatii, ce reprezinta pozitiile initiale ale bomboanelor speciale.

Date de iesire

Fisierul de iesire penal.out va avea M linii, fiecare continand P perechi de numere naturale separate prin spatii reprezentand pozitiile bomboanelor speciale dupa fiecare operatie. Ordinea bomboanelor pe fiecare linie trebuie sa fie aceeasi ca si in fisierul de intrare.

Restrictii

• 1 ≤ N ≤ 40000
• 1 ≤ P ≤ min(100, N²)
• 1 <= M <= 1000
• Pentru 30% din teste N ≤ 50, in timp ce pentru 60% dintre ele N <= 1000.
• Pozitiile bomboanelor speciale sunt valide. Nu exista doua bomboane speciale cu aceeasi pozitie.

Exemplu

Cum se trimit solutii?