Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | pastile.in, pastile.out | Sursă | OSEPI Baraj Seniori 2 |
| Autor | Bogdan Pop, Bogdan Sitaru | Adăugată de | |
| Timp execuţie pe test | 0.25 sec | Limită de memorie | 131072 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Pastile
Robert s-a plictisit de tricoul său alb, aşa că s-a hotărât să îl coloreze în culoarea sa preferată, albastru. El a primit de la prietenul său, Georgian, mai multe pastile de N nuanţe diferite de albastru, având acum pi pastile din cea de-a i-a nuanţă de albastru (pentru i de la 1 la N). Pentru a colora tricoul, Robert va pune tricoul în maşina de spălat alături de diverse pastile.
Plictisit de nuanţele obişnuite de albastru, el va crea o nouă nuanţă luând a1, ..., aN pastile (ai pastile din nuanţa iniţială i). Robert va lua cel puţin o pastilă din fiecare nuanţă iniţială, şi cel mult pi pastile din nuanţa i. De asemenea, el poate folosi doar un număr întreg de pastile din fiecare tip. Două nuanţe a1, ..., aN şi b1, ..., bN vor fi considerate la fel dacă şi numai dacă 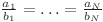 .
.
Acum, Robert se întreabă câte nuanţe noi diferite de albastru poate crea. Ştiind că acest număr poate fi foarte mare, el se mulţumeşte şi cu răspunsul modulo 1 000 000 007.
Date de intrare
Pe prima linie a fişierului de intrare pastile.in se găseşte un număr întreg N, reprezentând numărul de nuanţe distincte.
Pe cea de-a doua linie se găsesc N numere întregi p1 ... pN, reprezentând numărul de pastile disponibile din cea de-a i-a nuanţă iniţială.
Date de ieşire
În fişierul de ieşire pastile.out se va afişa o singură linie, ce conţine un singur număr întreg, reprezentând numărul de nuanţe diferite ce se pot forma modulo 1 000 000 007.
Restricţii
- Vom nota Vmin = min(p1, ..., pN) şi Vmax = max(p1, ..., pN).
- 1 ≤ N ≤ 200 000
- 1 ≤ Vmin ≤ Vmax ≤ 200 000
Punctare
| Subtask | Punctaj | Restricţii |
|---|---|---|
| 1 | 2 | Vmin = 1 |
| 2 | 6 | 1 ≤ N, Vmax ≤ 7 |
| 3 | 4 | 1 ≤ N, Vmax ≤ 8 |
| 4 | 16 | 1 ≤ N, Vmax ≤ 100 |
| 5 | 11 | 1 ≤ N, Vmax ≤ 1 000 |
| 6 | 7 | 1 ≤ N, Vmax ≤ 5 000 |
| 7 | 15 | 1 ≤ N, Vmax ≤ 30 000 |
| 8 | 10 | Vmin = Vmax |
| 9 | 8 | 1 ≤ Vmin ≤ 100 |
| 10 | 21 | Fără restricţii suplimentare. |
Exemplu
| pastile.in | pastile.out |
|---|---|
| 3 2 3 2 | 11 |
| 4 7 7 7 7 | 2303 |
| 7 15 8 19 7 15 8 19 | 36191027 |
| 2 31124 150719 | 851838928 |
Explicaţie
Pentru primul exemplu, cele 11 nuanţe posibile sunt:
- (1, 1, 1) (la fel cu (2, 2, 2))
- (1, 1, 2)
- (1, 2, 1)
- (1, 2, 2)
- (1, 3, 1)
- (1, 3, 2)
- (2, 1, 1)
- (2, 1, 2)
- (2, 2, 1)
- (2, 3, 1)
- (2, 3, 2)
