| Fişierul intrare/ieşire: | partitura.in, partitura.out | Sursă | OJI 2023, clasa a 9-a |
| Autor | Mihaela Cismaru | Adăugată de | |
| Timp execuţie pe test | 0.2 sec | Limită de memorie | 268288 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Partitura
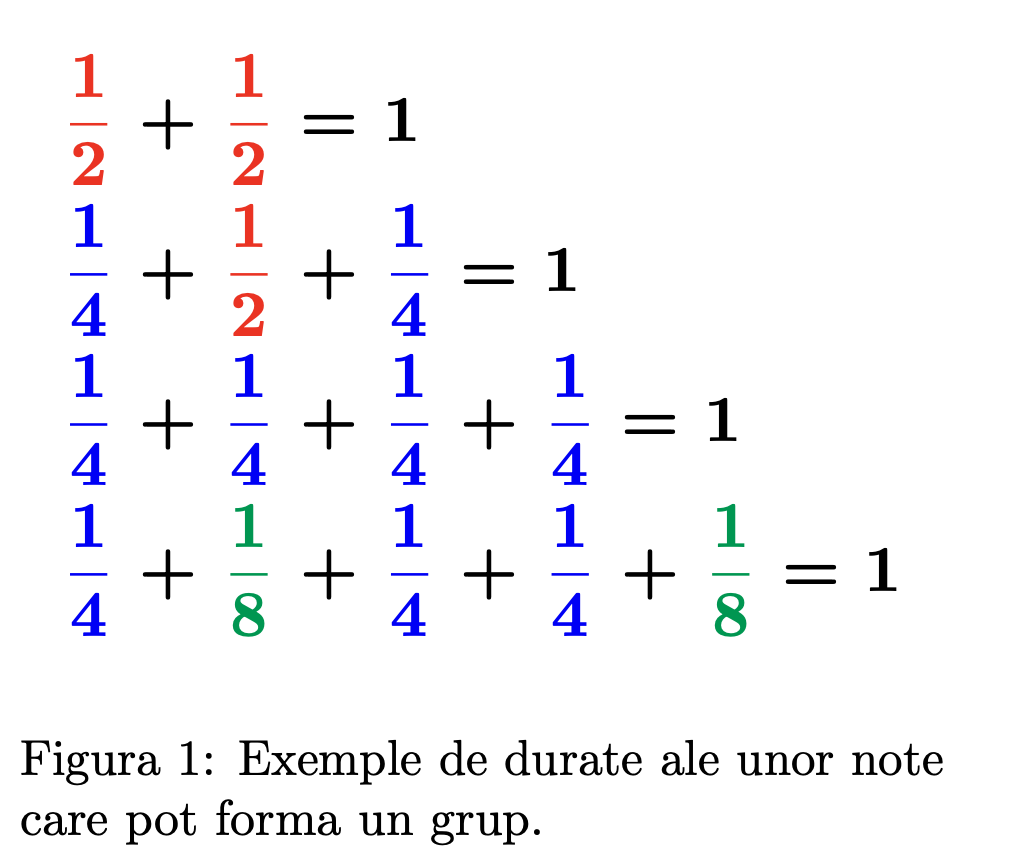
Mihai s-a decis în sfârşit să compună o melodie. Fără să ştie de unde să înceapă, a scris pe o foaie n note muzicale. Fiecare notă muzicală este definită de două valori reprezentând durata şi înălţimea acesteia astfel:
- durata este exprimată printr-o fracţie de forma 1/2x , unde x este un număr natural nenul
- înălţimea este exprimată printr-un număr natural nenul y
Durata unui grup de note este egală cu suma duratelor notelor din grup. Pentru a compune o melodie corect din punct de vedere muzical, el trebuie să distribuie toate notele în grupuri disjuncte, astfel încât durata fiecărui grup să fie 1. Mihai defineşte scorul unui grup de note ca fiind suma înălţimilor tuturor notelor din grup, ridicată la pătrat. De asemenea, el defineşte scorul unei melodii ca fiind suma scorurilor tuturor grupurilor de note formate pentru acea melodie. Mihai vrea să afle care este scorul maxim al unei melodii pe care îl poate obţine după gruparea tuturor notelor date.
Cerinţa
Dându-se n note sub forma a n perechi de numere, x şi y , să se afişeze scorul maxim ce poate fi obţinut după gruparea tuturor notelor date în grupuri disjuncte.
Date de intrare
Fişierul de intrare partitura.in va conţine pe prima linie un număr natural n, reprezentând numărul de note, iar pe următoarele n linii se vor afla câte două numere naturale x şi y separate prin câte un spaţiu, cu semnificaţia din enunţ, pentru fiecare din cele n note.
Date de ieşire
În fişierul de ieşire partitura.out va conţine un singur număr natural reprezentând scorul maxim cerut.
Restricţii
- 1 ≤ n ≤ 300 000
- 1 ≤ x ≤ 18
- 1 ≤ y ≤ 10 000
- Se garantează că se pot distribui toate notele date în grupuri de durată 1.
| # | Punctaj | Restricţii |
|---|---|---|
| 1 | 20 | n ≤ 4, x = 1 |
| 2 | 22 | x = 1 |
| 3 | 17 | Pentru toate notele, x are aceeaşi valoare |
| 4 | 41 | Fără restricţii suplimentare |
Exemple
| partitura.in | partitura.out |
|---|---|
| 5 2 3 3 2 2 1 2 2 3 5 | 169 |
| 6 1 3 2 2 1 4 2 2 2 2 2 2 | 113 |
Explicaţii
Exemplul 1
Pentru a determina scorul maxim al unei melodii, singura soluţie posibilă se obţine prin formarea unui singur grup. Acesta este format din toate notele şi are durata 1/22 + 1/23 + 1/22 + 1/22 + 1/23 = 1 şi scorul (3 + 2 + 1 + 2 + 5)2 = 169. Scorul melodiei este, de asemenea, 169.
Exemplul 2
Pentru a determina scorul maxim al unei melodii, o soluţie posibilă se obţine prin formarea a două grupuri. Primul grup este format din prima, a doua şi a patra notă şi are durata 1/2 + 1/22 + 1/22 = 1 şi scorul (3 + 2 + 2)2 = 49. Al doilea grup este format din a treia, a cincea şi a şasea notă şi are durata 1/2 + 1/22 + 1/22 = 1 şi scorul (4 + 2 + 2)2 = 64. Scorul melodiei este 49 + 64 = 113 şi este maximul care se poate obţine pentru aceste note.
