Fişierul intrare/ieşire:	operatii2.in, operatii2.out	Sursă	Lot Juniori 2009 - Baraj 2
Autor	Doru Popescu Anastasiu	Adăugată de	Gavrila Vlad •GavrilaVlad
Timp execuţie pe test	0.05 sec	Limită de memorie	20480 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Operatii2

Fiind date două tablouri bidimensionale a şi b, cu m linii şi n coloane fiecare, definim următoarele operaţii:

1. Suma tablourilor a şi b, ca fiind un tablou c cu m linii şi n coloane, în care fiecare element este egal cu suma elementelor de pe aceeaşi linie şi coloană din a şi b. În acest caz folosim operatorul +, adică c = a + b. 
2. Produsul tablourilor a şi b, ca fiind un tablou d cu m linii şi n coloane, in care fiecare element este egal cu produsul elementelor de pe aceeşi linie şi coloană din a şi b. În acest caz folosim operatorul *, adică d = a * b. Dacă a şi b sunt tablouri identice (a şi b au elemente identice pe aceeaşi poziţie), atunci pentru d se mai foloseşte şi notaţia a² sau b².

Exemplu:

Pentru m = 2, n = 3 şi tablourile:

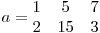 şi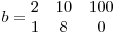 

Se obţine:

 ,  ,  ,  .

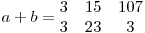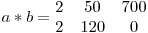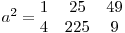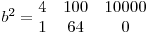Fiind dat un tablou bidimensional a, cu m linii, n coloane şi componente numere naturale dorim să determinăm un şir de tablouri bidimensionale: b₁, b₂, ..., b_k cu număr minim de termeni (k minim), cu proprietatea că a = b₁² + b₂² + ... + b_k².

Cerinţă 

Să se scrie un program care determină tablourile bidimensionale b₁, b₂, ..., b_k cu proprietatea din enunţ.

Date de intrare

Fişierul de intrare operatii.in conţine pe prima linie numerele naturale m şi n separate prin câte un spaţiu. Pe umătoarele m linii se află elementele tabloului a, câte n numere pe o linie, în cadrul unei linii numerele fiind separate între ele prin câte un spaţiu.

Date de ieşire

Fişierul de ieşire operatii.out conţine pe prima linie un număr natural reprezentând valoarea k, apoi pe următoarele k * m linii elementele celor k tablouri b₁, b₂, ..., b_k. Fiecare dintre aceste tablouri va fi scris pe câte m linii consecutive, iar pe fiecare dintre aceste linii se vor afla câte n numere separate prin câte un spaţiu.

Restricţii

• 1 ≤ m, n ≤ 200
• Componentele tabloului a sunt numere naturale ≤ 10 000.
• Pot exista mai multe solutii, dar în fişierul de ieşire se va scrie una dintre ele.
• 30% din teste au componentele tabloului a mai mici sau cel mult egale cu 100 şi m, n ≤ 100.
• 60% din teste au componentele tabloului a mai mici sau cel mult egale cu 1 000.

Exemplu

Explicaţie

a este:  .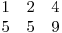

b₁ este: 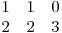 iar b₁² este: .

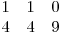b₂ este: 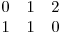 iar b₂² este: .

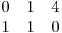Se observă că b₁² + b₂² = a.

Cum se trimit solutii?