| Fişierul intrare/ieşire: | norocoase.in, norocoase.out | Sursă | Sapientia ECN 2016 |
| Autor | Paul Diac | Adăugată de | |
| Timp execuţie pe test | 2.5 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Norocoase
Fie P un poligon convex cu N varfuri: ( x[i], y[i] ) unde ambele coordonate ale fiecărui punct sunt numere naturale. Poligonul se poate roti cu orice unghi.
După rotaţie se consideră cel mai de jos vârf: cel cu y[i] minim, fie aceasta valoare ymin. Toate punctele care au y[i] după rotaţie în intervalul [ymin, ymin + W] sunt norocoase, unde W este un număr natural dat.
Care este numărul maxim de vârfuri norocoase care se pot obţine rotind poligonul corespunzator?
Date de intrare
Fişierul de intrare norocoase.in conţine pe prima linie numărul de teste T. Urmează pe rând descrierea pentru fiecare test:
Prima linie numerele N şi W reprezentând numărul de vârfuri şi laţimea W.
Următoarele N linii conţin două numere naturale x[i] şi y[i], coordonatele iniţiale ale punctelor în ordine. Ordinea poate fi trigonometrică sau ordinea acelor de ceasornic.
Date de ieşire
În fişierul de ieşire norocoase.out afişaţi răspunsul pentru fiecare test în ordine: numărul maxim de puncte care pot fi norocoase după rotaţie.
Restricţii
- 1 ≤ T ≤ 10
- 3 ≤ N ≤ 105
- 0 ≤ x[i], y[i], W ≤ 109
- Rotaţia poate fi făcută cu un numar fracţionar de grade: se poate roti cu orice precizie.
Exemplu
| norocoase.in | norocoase.out |
|---|---|
| 1 8 3 9 1 11 5 9 10 5 11 3 9 2 7 2 4 3 2 | 5 |
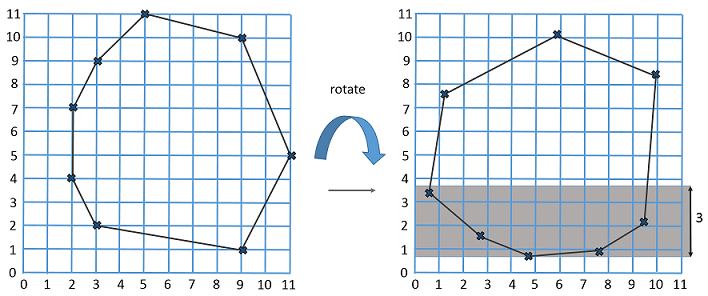
Explicaţie
Punctele cu coordonatele iniţiale (5, 11), (3, 9), (2, 7), (2, 4), (3, 2) pot fi norocoase: