Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | nambartiori.in, nambartiori.out | Sursă | Junior Challenge 2020 |
| Autor | Cezar Trisca-Vicol | Adăugată de |  Comisia •JuniorChallenge2020 |
| Timp execuţie pe test | 0.08 sec | Limită de memorie | 524288 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Nambartiori
Kokalaru47 şi-a dat seama că singurul mod de a face mulţi bani în viaţă este de a învăţa matematică. Dupa ce a studiat îndelungat tainele matematicii, acesta a ajuns la concluzia că "Nambăr Tiori" este capitolul lui preferat. Îi place atât de mult incât acesta a început în fiecare zi să îşi aşeze banii în grămezi astfel încât dacă ar scrie pe o foaie numărul de bani din fiecare grămadă, şirul rezultat ar fi o progresie geometrică de numere naturale. O progresie geometrică de lungime 
cu raţia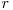 
este un şir de numere 
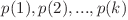pentru care se respectă relaţia : 
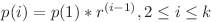. Din păcate, el fiind un kokalar adevărat, nu ţine cont de bani, iar după ce i-a aşezat într-o progresie geometrică a uitat numărul lor. Tot ce ţine minte despre progresia geometrică este că e a 
-a progresie geometrica de lungime cu raţia mai mare decât 
şi mai mică sau egală cu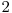 
în ordine lexicografică.
Cerinţă
Ştiind că acesta şi-a aşezat banii în T progresii geometrice ajutaţi-l să le gasească.
Date de intrare
Fişierul de intrare nambartiori.in conţine pe prima linie un număr natural T, reprezentând numărul de teste. Pe următoarele T linii, se vor găsi două numere n şi k, având semnificaţia din enunţ.
Date de ieşire
În fişierul de ieşire nambartiori.out se vor găsi T linii, pe fiecare linie i găsindu-se răspunsul la întrebarea i.
Restricţii
- T <= 10
- n <= 1.000.000.000
- 2 <= k <= 10
- Subtaskul 1 (10 puncte, testele 1-2): k = 2
- Subtaskul 2 (20 puncte, testele 3-4): n ≤ 100
- Subtaskul 3 (30 puncte, testele 5-6): n ≤ 10.000
- Subtaskul 4 (40 puncte, testele 7-10): Restricţiile iniţiale
Exemplu
| nambartiori.in | nambartiori.out |
|---|---|
| 10 1 4 2 4 3 4 4 4 5 4 6 4 7 4 8 4 9 4 10 4 | 1 2 4 8 2 4 8 16 3 6 12 24 4 8 16 32 5 10 20 40 6 12 24 48 7 14 28 56 8 12 18 27 8 16 32 64 9 18 36 72 |
| 5 5763 2 34568 7 9345 3 845689 6 1065354 4 | 107 199 33922 67844 135688 271376 542752 1085504 2171008 3105 6210 12420 810280 1620560 3241120 6482240 12964480 25928960 783083 1566166 3132332 6264664 |
Explicaţie
Primele 10 progresii geometrice de lungime 4 cu raţia cerută sunt :
1 2 4 8
2 4 8 16
3 6 12 24
4 8 16 32
5 10 20 40
6 12 24 48
7 14 28 56
8 12 18 27
8 16 32 64
9 18 36 72
10 20 40 80
