| Fişierul intrare/ieşire: | mergeheap.in, mergeheap.out | Sursă | arhiva educationala |
| Autor | Filipescu Radu, Mititelu Teodor | Adăugată de |  Filipescu Radu •Radu_Filipescu |
| Timp execuţie pe test | 0.15 sec | Limită de memorie | 65536 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Heapuri cu reuniune
Fie N mulţimi de elemente. Asupra acestor mulţimi se vor efectua 3 tipuri de operaţii.
- operaţia de tipul 1: în mulţimea m se inserează elementul x.
- operaţia de tipul 2: se afişează elementul maxim din mulţimea m, apoi se elimină din aceasta.
- operaţia de tipul 3: se reunesc mulţimile a şi b ( mulţimea a preia elementele mulţimii b, care rămâne vidă )
Date de intrare
Fişierul de intrare mergeheap.in va conţine pe prima linie valorile lui N şi Q, care reprezintă numărul de mulţimi pe care se vor face operaţiile, respectiv numărul de operaţii. Pe următoarele Q linii se va afla un număr care reprezintă tipul operaţiei, urmat apoi de o valoare, dacă tipul operaţiei este 2, respectiv de două valori pentru operaţiile 1 şi 3.
Date de ieşire
Fişierul de ieşire mergeheap.out va contine, pe câte o linie, răspunsul pentru fiecare operaţie de tipul 2 din fişierul de intrare, în ordinea data.
Restricţii
- 1 ≤ N ≤ 100
- 1 ≤ Q ≤ 300000
- Elementele mulţimilor sunt numere naturale, mai mici decât 2 000 000 000.
- Se garantează că nu se va cere operaţia 2 pentru o mulţime vidă.
Exemplu
| mergeheap.in | mergeheap.out |
|---|---|
| 5 10 1 2 5 1 1 3 1 3 7 1 3 4 1 2 2 2 2 3 2 1 2 2 3 3 2 2 3 | 5 3 7 |
Explicaţie
Primele 5 operaţii introduc elemente în mulţimi. La a 6-a operaţie trebuie afişat maximul din a doua mulţime, cea care conţine elementele 2 şi 5. Deci vom afişa 5 şi îl vom elimina din mulţimea sa. Apoi trebuie reunite a doua mulţime cu prima, a doua conţinând, dupa reuniune, elementele 2 şi 3. Apoi ni se cere să afişăm elementul maxim din această mulţime. Penultima operaţie este de reuniune dintre mulţimile 3 şi 2, urmată apoi de afişarea şi eliminarea maximului din aceasta.
Indicaţii de rezolvare
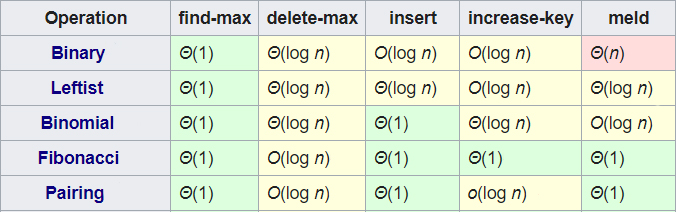
O soluţie simplă constă în folosirea unor heapuri binare, care sunt uşor de implementat şi vor efectua operaţiile de adăugare şi de eliminare în complexitate logaritmică. Problema acestora este operaţia de reuniune, care se efectuează în O(N*log 2 N), dacă introducem element cu element o mulţime în cealaltă, sau în O(N), folosind heapify pentru construirea unui heap, această soluţie va obţine aproximativ 30 de puncte.
Pentru a efectua mai rapid operaţia de reuniune, se pot folosi structuri de date precum Binomial Heap sau Pairing Heap, care efectuează operaţiile de tipul 3 în O(log 2 N), respectiv în O(1) amortizat. O sursă care implementează Binomial Heap puteţi vedea aici, aceasta va obţine în jur de 70 de puncte, şi una cu Pairing Heap aici., care va obţine punctajul integral.
Complexităţile operaţiilor pentru aceste structuri de date, precum şi câteva alternative ale acestora.
