Fişierul intrare/ieşire:	makebipartite.in, makebipartite.out	Sursă	InfoPro, Runda 2, Grupa A
Autor	Andrei Constantinescu	Adăugată de	Tamio Vesa Nakajima •tamionv
Timp execuţie pe test	2.5 sec	Limită de memorie	524288 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

MakeBipartite

Sile a învăţat la ora de matematică definiţia unui graf bipartit. Considerăm un graf neorientat G format dintr-o mulţime de noduri V şi o mulţime de muchii E. Spunem că G este bipartit dacă şi numai dacă există două submulţimi V¹, V² ale lui V astfel încât:

1. V¹ şi V² sunt disjuncte.
2. V¹ şi V² reunite sunt egale cu V.
3. fiecare muchie din E are o extremitate în V¹ şi o extremitate în V².

Sile a dat peste un graf neorientat G, cu nodurile V şi muchiile E, format din N noduri (V = {1, 2, ..., N}) şi M muchii (|E| = M). El se întreabă acum pentru care noduri v avem că graful G - v obţinut prin eliminarea nodului v şi a muchiilor incidente lui v din G este bipartit.

Voi va trebui sa îl ajutaţi pe Sile să îşi rezolve problema pentru T scenarii.

Date de intrare

Pe prima linie a fişierului de intrare makebipartite.in se va afla T, reprezentând numărul de scenarii.
Urmează apoi T grupe de linii, fiecare corespunzând câte unui scenariu, fiecare fiind descris după cum urmează:
Pe prima linie a scenariului se vor afla N şi M, separate printr-un spaţiu.
Pe următoarele M linii ale scenariului se vor afla câte două numere a b, separate printr-un spaţiu şi reprezentând câte o muchie (a, b) din E a grafului G din scenariul curent.

Date de ieşire

Se vor afişa T linii, câte una pentru fiecare scenariu, după cum urmează:

Pentru un scenariu răspunsul este reprezentat de un şir format din N caractere, fără spaţii între ele. Al i-ulea caracter din răspuns va fi 1 dacă G - i este bipartit, şi 0 altfel.

Resticţii

• Nu vor exista muchii cu a = b.
• Nu vor exista muchii care să apară de mai multe ori în cadrul aceluiaşi scenariu.
• Se consideră identice muchiile (a, b) şi (b, a).
• Fie SN suma lui N într-un fişier, şi SM suma lui M într-un fişier.
• 1 ≤ T ≤ 40.000
• 1 ≤ N ≤ 1.000.000
• 1 ≤ M ≤ 2.500.000
• SN ≤ 1.000.000.
• SM ≤ 2.500.000.
• Pentru 23 de puncte, T ≤ 600, N ≤ 2.000, M ≤ 5.000, SN ≤ 20.000, SM ≤ 20.000.
• Pentru alte 32 de puncte, T ≤ 20.000, N ≤ 100.000, M ≤ 250.000, SN ≤ 120.000, SM ≤ 350.000, şi se acorda punctaj oricarei surse care gaseste raspunsul corect cel putin pentru nodurile v din V pentru care exista maxim doua muchii incidente in G.
• Pentru alte 22 de puncte, T ≤ 20.000, N ≤ 100.000, M ≤ 250.000, SN ≤ 120.000, SM ≤ 350.000
• Se recomandă parsarea inputului.

Exemplu

Explicaţii

Avem T = 2 scenarii de rezolvat.

În primul scenariu graful G este cel din imaginea de mai jos.

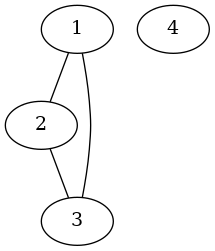
Observăm că nodurile 1, 2 şi 3 sunt vecine două câte două, de unde deducem că graful G nu este bipartit. Prin eliminarea oricăruia dintre nodurile 1, 2 sau 3, graful rezultat va fi bipartit. De exemplu, dacă am elimina nodul 2 (implicit şi muchiile sale incidente 2-1 şi 2-3), atunci graful rezultat G - 2 va fi bipartit, deoarece se pot alege submulţimile V¹ = {1, 4}, V² = {3} respectând proprietăţile din enunţ (n.b. există şi alte modalităţi de a alege mulţimile V¹, V²). Eliminarea nodului 4 nu ar duce la un graf bipartit. Aşadar, răspunsul pentru acest scenariu este 1110.

În al doilea scenariu graful G este cel din imaginea de mai jos.

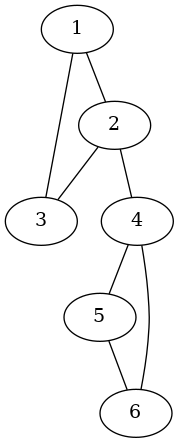
În acest caz, indiferent ce nod v din V s-ar elimina din G, graful rezultat G - v nu ar fi bipartit. Aşadar, răspunsul în acest caz este 000000.

Cum se trimit solutii?