Fişierul intrare/ieşire:	lru.in, lru.out	Sursă	Lot Baia Mare 2013 - Baraj 2 Seniori
Autor	Adrian Panaete, Alexandru Cazacu	Adăugată de	Daniel Constantin Anghel •Magnvs
Timp execuţie pe test	0.2 sec	Limită de memorie	65536 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Lru

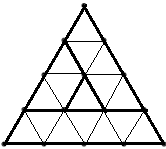
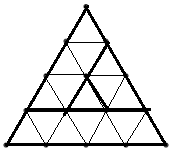
Adrian Wonder Boy tocmai a primit un joc nou. Acesta constă din n triunghiuri echilaterale situate în plan vertical având o latură orizontală şi vârful opus acesteia îndreptat în sus. Triunghiurile au laturile de lungime 1, 2, 3, …, n şi sunt incluse unul în altul astfel încât oricare două triunghiuri consecutive au un unghi comun. Mai precis, un triunghi mic (de latură i; în desen i=3) poate fi în exact urmatoarele 3 poziţii faţă de triunghiul mai mare (de latură i+1) :

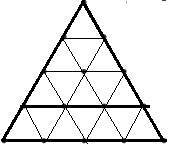L. triunghiul mic este “în stânga”.	R. triunghiul mic este “în dreapta”.	U. triunghiul mic este “sus”.

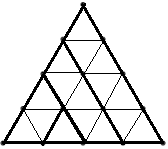
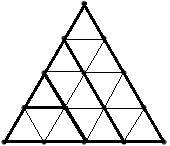
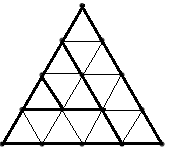
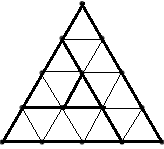
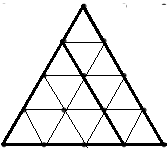
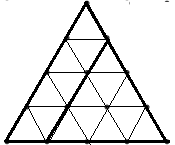
Starea jocului la un moment dat poate fi codificată printr-un şir de n-1 caractere ‘L’ , ‘R’ sau ‘U’ care descriu poziţia fiecărui triunghi de latura i (1<=i<n) faţă de triunghiul de latură i+1. De exemplu pentru n=4 în figurile de mai jos avem trei stări ale jocului împreună cu codificările acestora.

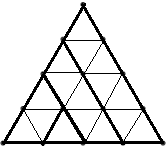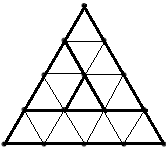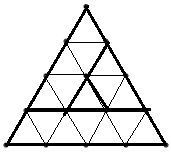Starea 1: RLL	Starea 2: RLU	Starea 3: LRU

Starea jocului poate fi modificată prin glisarea unuia dintre triunghiurile interioare pe direcţia uneia dintre laturi într-un sens sau altul, cu exact o unitate. De exemplu glisând orizontal spre dreapta triunghiul de latură 2 se poate trece din starea 2 în starea 3. Faţă de triunghiul de latură 3, triunghiul de latură 2 a trecut din stânga în dreapta. (Reţineţi faptul că prin glisarea unui triunghi cele interioare lui rămân pe poziţia veche, deci unele mutări nu sunt posibile. De exemplu, în starea 1 triunghiul de latură 2 nu poate glisa în sus deoarece triunghiul de latură 1 ar rămâne în afara triunghiului de latură 2)

Pentru mai multe teste, cunoscând n şi două stări ale jocului, să se determine numărul minim de glisări în urma cărora jocul trece din prima stare în a doua stare.

Date de intrare

Pe prima linie a fişierului lru.in avem un număr natural t - numărul de teste. Următoarele 3*t linii descriu cele t teste, un test pe câte 3 linii. Prima linie dintre cele 3 conţine un număr natural n – lungimea comună a codificării celor două stări. A doua linie dintre cele 3 conţine un şir de n caractere – codificarea stării iniţiale. A treia linie dintre cele 3 conţine un sir de n caractere – codificarea stării finale.

Date de ieşire

Fişierului lru.out va conţine t linii. Linia k (1<= k <= t) va conţine un număr natural m[k] – soluţia testului k din fişierul de intrare.

Restricţii

• 1 ≤ t ≤ 5
• 2 ≤ n ≤ 1 000 000
• Pentru 70% din teste, n ≤ 200 000

Exemplu

Explicaţie

Se efectuează 5 glisări şi jocul trece prin următoarele stări:
RLL -> ULL -> LUL -> RUL -> RLU -> LRU

Cum se trimit solutii?