Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | lgput.in, lgput.out | Sursă | ad-hoc |
| Autor | Arhiva Educationala | Adăugată de |  Tudorica Constantin Alexandru •tudalex |
| Timp execuţie pe test | 0.025 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Ridicare la putere in timp logaritmic
Dandu-se doua numere naturale N si P, se cere sa se calculeze restul impartirii lui NP la 1999999973.
Date de intrare
Fisierul de intrare lgput.in va contine 2 numere N si P.
Date de iesire
In fisierul de iesire lgput.out va fi scris un singur numar reprezentand restul impartirii lui NP la 1999999973.
Restrictii
- 2 ≤ N, P ≤ 232
Exemplu
| lgput.in | lgput.out |
|---|---|
| 2 4 | 16 |
Indicatii de rezolvare
O solutie directa este cea prin inmultiri repetate. Aceasta solutie are complexitatea O(P) si obtine 30 de puncte.
O alta solutie este cea de a ridica la putere in timp logaritmic si are o complexitatea O(log2P). Descrierea acestui procedeu se gaseste pe wikipedia. Algoritmul se poate aplica si la matrici si polinoame.
Sursa de 100 de puncte se gaseste aici.
Utilizari
Pentru determinarea inversul numarului x modulo un numar prim p: teorema mica a lui fermat ne spune ca x(p-1) modulo p = 1. De aici avem ca inversul lui x este x(p-2) pe care il putem calcula rapid folosind exponentiere rapida. O cale mai generala de a determina inversul unui numar x modulo un numar n, unde n nu este neaparat prim, ar fi folosirea algoritmului lui Euclid extins.
Alta tip de probleme unde exponentierea rapide ne este utila ar fi determinarea rapida a valorii modulo n a unui element a[k] unde a este un sir definit printr-o recurenta liniara.
De exemplu daca sirul a[k] = x a[k - 1] + y a[k - 2] + z a[k - 3], atunci putem defini vectorul (a[k], a[k - 1] , a[k - 2]) fiind dat de inmultirea vectorului (a[k - 1], a[k - 2], a[k - 3) cu matricea A: 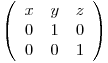![\left( \begin{array}{ccc}
x & y & z \
0 & 1 & 0 \
0 & 0 & 1 \end{array} \right)](http://www.infoarena.ro/static/images/latex/32a76724f9675d7f99ccbfdd3d571c44_16.50017pt.gif "\left( \begin{array}{ccc}
x & y & z \
0 & 1 & 0 \
0 & 0 & 1 \end{array} \right)")
Si atunci pentru a determina a[k] modulo n rapid, putem folosi ridicarea la putere a matricii A.
