Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | kfib.in, kfib.out | Sursă | Arhiva Educationala |
| Autor | Arhiva Educationala | Adăugată de | |
| Timp execuţie pe test | 0.025 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Al k-lea termen Fibonacci
Fie şirul lui Fibonacci, dat prin 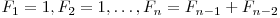 .
.
Cerinţă
Să se calculeze al K-lea termen al şirului modulo 666013.
Date de intrare
Fişierul de intrare kfib.in conţine o singură linie cu numărul natural K.
Date de ieşire
În fişierul de ieşire kfib.out se va afişa al K-lea termen al şirului modulo 666013.
Restricţii
- 1 ≤ K ≤ 1 000 000 000.
Exemplu
| kfib.in | kfib.out |
|---|---|
| 5 | 5 |
| 2707124 | 660634 |
Indicaţii pentru rezolvare
O implementare directă a relaţiei de recurenţă în complexitate liniară ar trebui să obţină 20 de puncte şi se găseşte aici.
Pentru a obţine 100 de puncte trebuie găsită o metoda mai eficientă de a rezolva această recurenţă. Ne vom folosi de înmulţirea matricilor în felul următor: la pasul 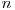 vom avea deja calculate
vom avea deja calculate 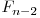 şi
şi 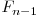 şi vrem să îl aflăm pe
şi vrem să îl aflăm pe 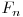 :
:
![\emph{}
\[\left( \begin{array}{ccc}
F_n-2_ & F_n-1_ \end{array} \right)\] & \times
\emph{}
\[\left( \begin{array}{ccc}
F_n-2_ & F_n-1_ \end{array} \right)\] & \times](http://www.infoarena.ro/static/images/latex/58bc40a25653d84ccff297650073cd78_4.50006pt.gif)
![\emph{}
\[ \left( \begin{array}{ccc}
0 & 1 \
1 & 1 \end{array} \right)\] = \emph{}
\[ \left( \begin{array}{ccc}
F_n-1_ & F_n_ \end{array} \right)\]
\emph{}
\[ \left( \begin{array}{ccc}
0 & 1 \
1 & 1 \end{array} \right)\] = \emph{}
\[ \left( \begin{array}{ccc}
F_n-1_ & F_n_ \end{array} \right)\]](http://www.infoarena.ro/static/images/latex/8c5e0790d2df5a793d854589d7a8bd77_10.50012pt.gif)
Vom nota cu Mi matricea ![\emph{}
\[ \left( \begin{array}{ccc}
F_i-1_ & F_i_ \end{array} \right)\]
\emph{}
\[ \left( \begin{array}{ccc}
F_i-1_ & F_i_ \end{array} \right)\]](http://www.infoarena.ro/static/images/latex/af40cd7e6fa5593b9b91e5a85e813301_4.50006pt.gif) iar cu Z matricea constantă,
iar cu Z matricea constantă, ![\emph{}
\[ \left( \begin{array}{ccc}
0 & 1 \
1 & 1 \end{array} \right)\] \emph{}
\[ \left( \begin{array}{ccc}
0 & 1 \
1 & 1 \end{array} \right)\]](http://www.infoarena.ro/static/images/latex/d9b9cdccb20ed7b37018315c0083aafc_10.50012pt.gif) .
.
Stim ca 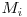 este egal cu
este egal cu 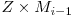 si mai stim ca
si mai stim ca 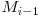 este egal cu
este egal cu  . Din proprietatea de asociativitate a inmultirii matricilor rezulta ca Mi este egal cu Z2 * Mi-2. Inductiv rezulta ca Mi = ZN-1 * M1. Soluţia optima se foloseşte de ridicarea la putere în timp logaritmic, avand complexitatea finala de O(log K * CONST). CONST este numarul de operatii efectuate la fiecare pas al ridicarii la putere si este egal cu dimensiunea matricii constante la puterea a 3-a, adica 8.
. Din proprietatea de asociativitate a inmultirii matricilor rezulta ca Mi este egal cu Z2 * Mi-2. Inductiv rezulta ca Mi = ZN-1 * M1. Soluţia optima se foloseşte de ridicarea la putere în timp logaritmic, avand complexitatea finala de O(log K * CONST). CONST este numarul de operatii efectuate la fiecare pas al ridicarii la putere si este egal cu dimensiunea matricii constante la puterea a 3-a, adica 8.
Aplicaţii
- Iepuri
- Hprob
- Nice Patterns Strike Back, SGU
- Tour Counting, Topcoder
- Ecu
- Pkinv
- Recurenta2
- Nr2
 Poti vedea testele pentru aceasta problema accesand
Poti vedea testele pentru aceasta problema accesand 