Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | inversmodular.in, inversmodular.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de |  dragus marius •mariusdrg |
| Timp execuţie pe test | 0.025 sec | Limită de memorie | 5120 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Invers modular
Se dau doua numere N si P, cu 1 ≤ N ≤ P-1, N si P sunt prime intre ele (cmmdc(N,P) = 1). Sa se determine X intre 1 si P-1 astfel incat N * X sa fie congruent cu 1, modulo P (restul impartirii lui N * X la P sa fie 1). Numarul X se va numi inversul modular al lui N.
Date de intrare
Fisierul de intrare inversmodular.in va contine pe prima linie numerele N si P, separate printr-un spatiu.
Date de ieşire
Fisierul de iesire inversmodular.out va contine pe prima linie numarul X cu proprietatea din enunt.
Restricţii
- 1 ≤ P ≤ 2.000.000.000
- 1 ≤ N ≤ P-1
- Pentru primele 70% din teste P este prim.
Exemplu
| inversmodular.in | inversmodular.out |
|---|---|
| 5 7 | 3 |
Explicaţie
5 * 3 este congruent cu 1, modulo 7, deoarece restul impartirii lui 15 la 7 este 1.
Indicaţii de rezolvare
Un algoritm evident ar fi incercarea tuturor numerelor X intre 1 si P-1 si verificarea proprietatii din enunt pentru X. O astfel de solutie are complexitatea O(P) si obtine 30 de puncte. Sursa se poate gasi aici.
Complexitatea optima pentru determinarea inversului modular este O(log2P). Din mica teorema a lui Fermat stim ca Xphi(P) = 1(%P), pentru orice numar P si X, pentru care se respecta conditia ca X e relativ prim cu P. Demonstratia acestei teoreme se bazeaza pe teoria grupurilor.
Din teorema rezulta ca Xphi(P) = X * Xphi(P)-1 este congruent cu 1, modulo P, deci Xphi(P)-1 este inversul modular al lui X. Solutia problemei va fi deci Xphi(P)-1 modulo P. Putem folosi exponentierea in timp logaritmic pentru a calcula Xphi(P)-1 modulo P in complexitate O(log2P).Pentru determinarea lui phi(P), avem complexitate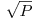 
. Pentru cazul particular cand P este prim, phi(P) = P - 1, deci raspunsul va fi XP-2. In acest caz, inversul modular se obtine in complexitate O(logP). O implementare ce se bazeaza pe aceasta idee se gaseste aici.
O alta abordare optima se bazeaza pe principiul extins al lui Euclid: oricare ar fi N si P numere intregi exista doua numere intregi A si B astfel incat A * N + B * P = cmmdc(N, P). Cum in problema determinarii inversului modular avem cmmdc(N,P)=1, exista A si B astfel incat A * N + B * P = 1. Considerand ecuatia modulo P, deoarece B * P este divizibil cu P, avem A * N congruent cu 1 (modulo P), deci A este inversul modular pentru N. Complexitatea acestui algoritm este tot O(log2P), deoarece coeficientii A si B pot fi determinati in timp logaritmic. A poate sa fie si negativ, deci trebuie sa adaugam P la A pana devine pozitiv. O astfel de solutie se poate gasi aici.
Aplicatii
- Stand in Line (uva)
- functii
