Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2009-12-05 19:31:25.
Revizia anterioară Revizia următoare

Fişierul intrare/ieşire:	huffman.in, huffman.out	Sursă	Arhiva Educationala
Autor	Arhiva Educationala	Adăugată de	Gavrila Vlad •GavrilaVlad
Timp execuţie pe test	0.5 sec	Limită de memorie	65536 kbytes
Scorul tău	N/A	Dificultate	N/A

Coduri Huffman

Codurile Huffman reprezintă o tehnică foarte eficientă de compactare a datelor, spaţiul economisit fiind cuprins adesea între 20% şi 90%. Algoritmul greedy pentru realizarea acestei codificări înregistrează frecvenţele de apariţie ale fiecărui simbol dintr-un fişier, după care utilizează o modalitate optimă pentru reprezentarea fiecărui simbol sub forma unui şir binar.

Astfel, se dă o mulţime A = {a₁,a₂,...,a_n} formată din n simboluri. Numim cod binar un şir de cifre de 0 şi 1 de o lungime finită. Fie B un şir de lungime n de coduri binare cu proprietatea că niciun cod b_i nu este prefixul unui alt cod b_j (i ≠ j).

Cerinţă

Ştiindu-se că într-un text T simbolul a_i apare de v_i ori, să se determine un şir B astfel încât înlocuind în textul T fiecare simbol a_i cu codul b_i să se obţină un text T' de lungime minimă lg.

Date de intrare

Fişierul de intrare huffman.in va conţine pe prima linie numărul natural n. Pe următoarele n linii se vor afla elementele şirului V, în ordine crescătoare.

Date de ieşire

În fişierul de ieşire huffman.out se va afişa pe prima linie lungimea minimă lg a textului T'. Pe următoarele n linii se vor afişa câte două numere naturale caracterizând elementele şirului B: lungimea fiecărui cod şi reprezentarea sa în baza 10.

Restricţii

1 ≤ n ≤ 1 000 000.
1 ≤ v_i ≤ 100 000 000.
1 ≤ lg ≤ 10¹⁸.
b_i ≤ 10¹⁸, 1 ≤ i ≤ N.
Soluţia nu este unică; poate fi afişată orice soluţie ce duce la o lungime lg minimă.

Exemplu

huffman.in	huffman.out
16 1 1 1 1 1 1 2 2 2 2 2 2 3 4 4 7	x

Explicaţie

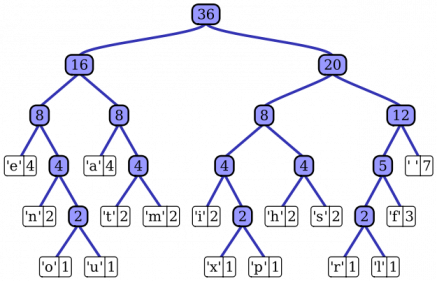
Pentru a materializa exemplul, am atribuit simboluri frecvenţelor date. Arborele Huffman obţinut se poate vedea în figura alăturată.

Simbolurile, împreună cu frecvenţele şi codificările aferente se găsesc în tabelul următor:

Lungimea totală a textului T' este 135, valoare ce se obţine însumând valorile tuturor nodurilor albastre.

Soluţie

Problema se rezolvă printr-un algoritm greedy, codarea Huffman. Se pot considera cele N caractere noduri într-un graf, având fiecare un cost egal cu numărul de apariţii al caracterului în textul T. La fiecare pas se creeaza un nod nou şi se duc de la acesta 2 muchii către nodurile de cost minim care nu au fost încă unite, costul acestuia fiind egal cu suma costurilor celor 2 fii. Pentru a putea reconstitui ulterior codurile, se asociaza celor 2 muchii valoarile 0 şi 1. Se va obţine un arbore binar cu 2*N-1 noduri, suma costurilor nodurilor interne fiind egală cu lungimea textului T'.
Algoritmul se poate generaliza pentru coduri in baza K, selectand la fiecare pas cele mai mici K noduri pentru a le uni cu nodul nou creat. De asemenea, trebuie create caractere fictive cu 0 aparitii, pentru ca numărul iniţial de noduri să fie de forma X * (K-1) + 1.

Etape de rezolvare

O soluţie în care căutarea celor 2 noduri de cost minim se face liniar are o complexitate O(N²) şi obţine 30 de puncte. Folosind un heap pentru a extrage nodurile de cost minim, complexitatea scade la O(N log~2~ N). Această soluţie obţine 70 de puncte. În cazul în care costurile nodurilor sunt date în ordine crescătoare, se pot ţine 2 cozi, conţinând nodurile iniţiale, respectiv nodurile interne. Observând că nodurile sunt sortate crescător după cost, se pot extrage cele 2 minime şi introduce nodul nou în O(1). Această soluţie obţine 100 de puncte.