| Fişierul intrare/ieşire: | harti.in, harti.out | Sursă | ad-hoc |
| Autor | Adăugată de | ||
| Timp execuţie pe test | 0.2 sec | Limită de memorie | 262144 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Hărți
Lorena, surioara Mirunei, a învăţat recent la cercul de informatică că orice hartă poate fi colorată folosind maxim patru culori. Cum fetiţa nu s-a lăsat convinsă în lipsa unei demonstraţii ea a petrecut ultimele două săptămâni încercând să găsească un contraexemplu. Într-un final, plictisită de atâta muncă fără rezultate, a decis ca se va mulţumii cu a demonstra proprietatea pe un caz mult mai particular. Astfel s-a născut următoarea problemă:
Fie un graf cu noduri de forma (xi, yi) în care oricare două muchii nu se intersectează decât, eventual, într-unul dintre capete. Orice muchie u-v respectă una dintre următoarele condiţii:
- xv = xu
- yv = yu
- |xv - xu| = |yv - yu|
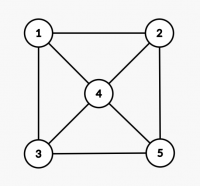
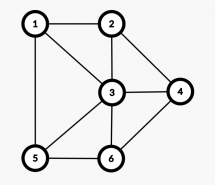
Găsiţi o colorare a nodurilor grafului, care foloseşte maxim K culori, astfel încât să nu existe două noduri cu aceeaşi culoare conectate print-o muchie.
Date de intrare
Fişierul de intrare harti.in va avea următorul format:
N M K
x1 y1
x2 y2
...
xN yN
u1 v1
...
uM vM
Pe prima linie se află trei numere, N, M şi K, reprezentând numărul de noduri, numărul de muchii şi, respectiv, numărul culorilor disponibile.
Nodurile sunt numerotate de la 1 la N.
Pe următoarele N linii vor fi câte două numere, xi şi yi, reprezentând coordonatele nodului i.
Pe următoarele M linii vor fi câte două numere, ui şi vi cu semnificaţia că există o muchie între nodurile ui şi vi.
Date de ieşire
În fişierul de ieşire harti.out se vor afişa N linii. Pe a i-a linie se va afla un număr cuprins între 1 şi K, culoarea nodului $$i.
Restricţii
- 1 ≤ N ≤ 2 000
- 1 ≤ M ≤ 5 000
- 0 ≤ xi, yi ≤ 1 000, pentru orice 1 ≤ i ≤ N
- 1 ≤ ui, vi ≤ N, pentru orice 1 ≤ i ≤ M
- ui ≠ vi, pentru orice 1 ≤ i ≤ M
- Nodurile sunt distincte două câte două.
- Muchiile sunt distincte două câte două (nu există muchii duble).
- Nu există muchie de la un nod la el însuşi.
- Se garanteaza ca exista solutie.
Subtaskuri
| Indice | Punctaj | Restricţii |
|---|---|---|
| 1 | 10 puncte | K = 9 |
| 2 | 15 puncte | K = 6 |
| 3 | 25 puncte | K = 5 |
| 4 | 50 puncte | K = 4 |
Exemplu
| harti.in | harti.out |
|---|---|
| 5 8 4 0 2 2 2 0 0 1 1 2 0 1 2 1 3 1 4 2 4 2 5 3 4 3 5 4 5 | 1 2 2 3 1 |
| 6 10 5 0 2 1 2 1 1 2 1 0 0 1 0 1 2 1 3 1 5 2 3 2 4 3 4 5 6 5 3 6 3 6 4 | 1 2 3 4 2 1 |
