Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | hamilton.in, hamilton.out | Sursă | Arhiva Educationala |
| Autor | Arhiva Educationala | Adăugată de |  Paul-Dan Baltescu •pauldb |
| Timp execuţie pe test | 0.375 sec | Limită de memorie | 36864 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Ciclu hamiltonian de cost minim
Se dă un graf orientat simplu cu N vârfuri şi M muchii, fiecare arc având asociat un cost. Un ciclu al acestui graf se numeşte hamiltonian dacă conţine fiecare nod din graf exact o singură dată. Un graf care conţine un astfel de ciclu se numeşte graf hamiltonian. Costul unui ciclu este egal cu suma arcelor aflate pe ciclu.
Cerinta
Fiind dat un graf orientat simplu cu costuri pe arce, să se verifice dacă acesta este hamiltonian. In caz afirmativ, să se determine ciclul hamiltonian de cost minim.
Date de intrare
Pe prima linie a fişierului de intrare hamilton.in se afla două numere întregi N si M. Pe fiecare din următoarele M linii se găseşte un triplet de forma x y c cu semnificaţia că există un arc între vârfurile x şi y având costul c.
Date de ieşire
Pe prima linie a fişierului de ieşire hamilton.out se va afla costul ciclului cerut. În cazul în care graful nu este hamiltonian, atunci în fişierul de ieşire se va afişa "Nu exista solutie".
Restricţii
- 1 ≤ N ≤ 16
- 1 ≤ M ≤ N*(N-1)
- Nodurile sunt numerotate de la 0 la N-1.
- Costurile arcelor sunt numere întregi cuprinse in intervalul [1, 1 000 000].
Exemplu
| hamilton.in | hamilton.out |
|---|---|
| 5 10 0 1 9 0 3 8 1 0 7 1 2 1 1 4 3 2 0 5 2 4 4 3 2 6 4 3 7 4 1 1 | 26 |
Explicaţie
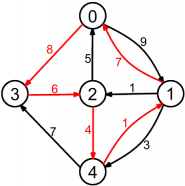
Ciclul hamiltonian de cost minim din exemplu este: 0 3 2 4 1 0. Un alt ciclu hamiltonian este 0 1 4 3 2 0, dar acesta are cost 30.
Indicaţii de rezolvare
O primă soluţie se bazează pe generarea tuturor permutărilor mulţimii {0, ..., N-1}. Pentru fiecare permutare generată {p1, ..., pN} se verifică dacă există arcele (p1 p2) (p2 p3) ... (pN-1 pN) (pN p1), iar în caz afirmativ se verifică dacă suma acestora este mai mică decât soluţia până la acest pas. Această soluţie are complexitate timp O(N!) şi obţine 20 de puncte. O sursă demonstrativă se găseşte aici.
Se observă că soluţia prezentată anterior nu verifică existenţa arcelor decât când întreaga permutare este generată. Această verificare se poate face în timpul generării permutării şi astfel se poate îmbunătăţi timpul de rulare. Această abordare se poate implementa şi sub forma unei parcurgeri în adâncime care generează toate lanţurile din graf; în cazul în care se determină un lanţ cu N noduri este verificată condiţia de închidere a ciclului (adică dacă există arcul dintre ultimul nod din lanţ şi nodul de start). În caz afirmativ, se verifică dacă ciclul găsit are un cost mai mic decât soluţia curentă. Acestă abordare are tot complexitate O(N!), dar timpul de rulare este mai bun. O implementare a acestui algoritm se găseşte aici şi obţine 40 de puncte.
Aplicaţii
Pentru a vă consolida cunoştinţele privind algoritmul prezentat in această problemă, vă recomandăm să rezolvaţi următoarele probleme:
