Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | generatoare.in, generatoare.out | Sursă | Concursul National Urmasii lui Moisil 2011 - Clasele 11 - 12 |
| Autor | Tudose Vlad Andrei | Adăugată de |  Andrici Cezar •andrici_cezar |
| Timp execuţie pe test | 0.1 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate |   3/5 |
Vezi solutiile trimise | Statistici
Generatoare
Avem n generatoare de numere notate G1, G2, ..., Gn. Generatorul Gi generează aleator un număr natural ai cuprins între 0 şi mi-1, fiecare număr având aceeaşi probabilitate de a fi generat. Notăm cu vxor valoarea a1 xor a2 xor ... xor an. Să se determine “valoarea aşteptată” pentru vxor ştiind că aceasta este egală cu suma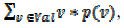 
, unde cu Val am notat mulţimea valorilor ce pot fi obţinute pentru vxor iar cu p(v) am notat probabilitatea ca valoarea obţinută pentru vxor să fie v.
Scrieţi un program care să determine “valoarea aşteptată” pentru vxor.
Date de intrare
Pe prima linie a fişierului de intrare generatoare.in se află numărul natural n reprezentând numărul de generatoare. Pe următoarele n linii se află numerele m1, m2, ..., mn, câte unul pe o linie. Mai exact, pe linia i+1 se află valoarea mi.
Date de ieşire
Fişierul de ieşire generatoare.out va conţine o singură linie pe care se află “valoarea aşteptată” pentru vxor cu exact 3 zecimale cu rotunjire.
Restricţii
- 1 ≤ n ≤ 50000
- 2 ≤ mi ≤ 230
- Pentru două numere naturale a şi b, definim a xor b valoarea obţinută aplicând operatorul „sau exclusiv” pe reprezentările binare ale lui a şi b.
Exemplu
| generatoare.in | generatoare.out |
|---|---|
| 2 3 5 | 2.200 |
Explicaţie
Avem două generatoare. Primul poate genera numerele 0, 1, 2 iar al doilea numerele 0, 1, 2, 3, 4. Deci perechea (a1,a2) poate avea următoarele valori: (0,0),(0,1),(0,2),(0,3),(0,4),(1,0),(1,1),(1,2),(1,3),(1,4),(2,0),(2,1),(2,2),(2,3),(2,4). Rezultă în ordine următoarele 15 valori pentru vxor 0,1,2,3,4,1,0,3,2,5,2,3,0,1,6. Observăm că valorile distincte posibile pentru vxor sunt 0,1,2,3,4,5 şi 6. Astfel, valorile 0,1,2 şi 3 au probabilitatea de apariţie 3/15 iar 4,5 şi 6 au probabilitatea de apariţie 1/15. Deci, “valoarea aşteptată” pentru vxor este (0+1+2+3)*(3/15)+(4+5+6)*(1/15) = 2.
