Fişierul intrare/ieşire:fibofrac.in, fibofrac.outSursăONI 2019, clasa a 9-a, ziua 2
AutorCiprian ChescaAdăugată deAlexPop28Pop Alex-Nicolae •AlexPop28
Timp execuţie pe test0.3 secLimită de memorie65536 kbytes
Scorul tăuN/ADificultateN/A

Vezi solutiile trimise | Statistici

Fibofrac

Fie şirul Fibonacci dat prin F1 = 1,F2 = 1 şi relaţia de recurenţă Fk = Fk-1 + Fk-2, k ≥ 3.
Se consideră un număr natural N.

Cerinţă

Să se scrie un program care determină numărul F al fracţiilor diferite ireductibile subunitare, ce se pot forma utilizând primii N termeni ai şirului Fibonacci.

Date de intrare

Fişierul de intrare fibofrac.in conţine pe prima linie numărul N.

Date de ieşire

Fişierul de ieşire fibofrac.out va conţine pe prima linie numărul F, cu semnificaţia de mai sus.

Restricţii

  • Pentru teste în valoare de 24 puncte, 0 < N < 80
  • Pentru teste în valoare de 40 puncte, 0 < N < 1 101
  • Pentru teste în valoare de 56 puncte, 0 < N < 50 001
  • Pentru teste în valoare de 100 puncte, 0 < N < 1 000 000
  • Două fracţii ireductibile a / b şi c / d sunt diferite dacă a ≠ c sau b ≠ d.
  • 0 ≤ F < 263

Exemplu

fibofrac.infibofrac.outExplicaţie
7
14
N=7;
Primii 7 termeni ai şirului Fibonacci
sunt: 1, 1, 2, 3, 5, 8, 13
Se pot forma 14 fracţii diferite
ireductibile subunitare: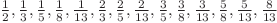
\frac{1}{2}, \frac{1}{3}, \frac{1}{5}, \frac{1}{8}, \frac{1}{13}, \frac{2}{3}, \frac{2}{5}, \frac{2}{13}, \frac{3}{5}, \frac{3}{8}, \frac{3}{13}, \frac{5}{8}, \frac{5}{13}, \frac{8}{13}
2019
1547722
Se pot forma 1547722 fracţii diferite
ireductibile subunitare utilizând primii
2019 termeni ai şirului Fibonacci.
500000
94988288219
Se pot forma 94988288219 fracţii diferite
ireductibile subunitare utilizând primii
500000 termeni ai şirului Fibonacci.
Trebuie sa te autentifici pentru a trimite solutii. Click aici

Cum se trimit solutii?