| Fişierul intrare/ieşire: | fft2d.in, fft2d.out | Sursă | ONI 2018, Baraj |
| Autor | Andrei Constantinescu | Adăugată de | |
| Timp execuţie pe test | 1.5 sec | Limită de memorie | 262144 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Fft2d
Un graf FFT de ordin F este un graf orientat cu F niveluri, numerotate de la 0 la F - 1. Fiecare nivel este compus din 2F - 1 noduri, numerotate cu numere de la 0 la 2F - 1 - 1. Vom folosi notaţia (h, x) pentru a ne referi la nodul cu indicele x de pe nivelul h.
Muchiile grafului FFT sunt următoarele:
- Toate muchiile orientate de la (h, x) la (h + 1, x);
- Toate muchiile orientate de la (h, x) la (h + 1, x ^ 2F - h - 2).
Iniţial toate nodurile grafului au fost colorate de Stiuboss cu alb. De supărare, Nustiuboss a selectat T noduri pe care le-a colorat cu negru. (Vedeţi figura)
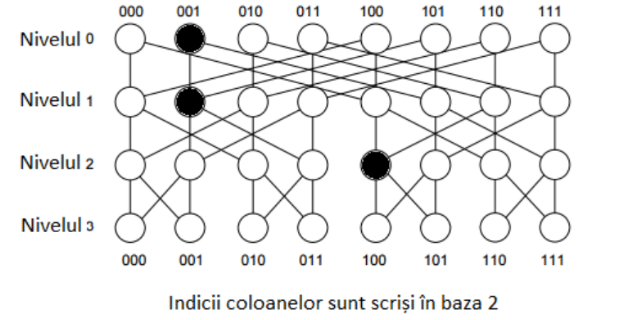
Intrigat de modificările făcute, Nusdeaici s-a decis să calculeze numărul de perechi (a, b) cu proprietatea că există măcar un drum orientat de la nodul (0, a) la nodul (F - 1, b) care nu trece prin niciun nod negru.
Date de intrare
Fişierul de intrare fft2d.in va conţine pe prima linie două numere naturale F şi T. Următoarele T linii vor conţine câte o pereche (h, x), reprezentând faptul că nodul de pe nivelul h cu indicele x este colorat cu negru.
Date de ieşire
Fişierul de ieşire fft2d.out va conţine un singur număr natural reprezentând numărul de perechi (a, b) cu proprietatea că există măcar un drum orientat de la nodul (0, a) la nodul (F - 1, b) care nu trece prin niciun nod negru.
Restricţii
- 1 ≤ F ≤ 30
- 1 ≤ T ≤ 100 000
- ATENŢIE! Muchiile sunt orientate (deşi în figură nu sunt reprezentate astfel)
- Pentru teste în valoare de 10 puncte, F ≤ 10
- Pentru alte teste în valoare de 10 puncte, F ≤ 16
- Pentru alte teste în valoare de 30 puncte, T ≤ 2 000
- “Apam, cum să numim personajul principal?” Răspuns: “Nustiuboss”.
Exemplu
| fft2d.in | fft2d.out | explicatii |
|---|---|---|
| 3 3 0 2 1 1 2 3 | 5 | Există 5 perechi (a, b) cu proprietatea din enunţ. Mai exact, acestea sunt: (0, 0), (0, 1), (0, 2), (1, 2), (3, 2). |
| 4 3 0 1 1 1 2 4 | 44 | Există 44 de perechi (a, b) cu proprietatea din enunţ. Figura din enunt corespunde acestui exemplu. |
| 15 10 3 12914 8 10479 12 1039 8 13597 11 2633 12 10668 12 6769 11 4443 7 15697 12 13418 | 268271648 | Va trebui să ne credeţi pe cuvânt. |
