Pagini recente » Diferente pentru problema/centrale intre reviziile 8 si 9 | Diferente pentru problema/valuare intre reviziile 12 si 76 | Diferente pentru problema/pandemie intre reviziile 4 si 39 | Diferente pentru problema/cai2 intre reviziile 9 si 12 | Dag

Atenţie! Aceasta este ultima versiune a paginii, scrisă la 2019-08-05 14:34:13.
Revizia anterioară Revizia următoare

Fişierul intrare/ieşire:	dag.in, dag.out	Sursă	ONI 2019, baraj
Autor	Mihai Calancea	Adăugată de	Tinca Matei •TincaMatei
Timp execuţie pe test	0.1 sec	Limită de memorie	524288 kbytes
Scorul tău	N/A	Dificultate	N/A

Dag

Un graf aciclic orientat (DAG - Directed Acyclic Graph) este un graf orientat fără cicluri.

Fie 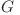$G$ un graf orientat aciclic simplu (adică nu conţine muchii multiple între aceleaşi noduri sau muchii de la un nod la el însuşi) în care nodurile sunt etichetate cu primele N numere naturale.

O sortare topologică a nodurilor unui graf aciclic orientat 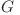$G$ este o ordonare a nodurilor astfel încât, dacă există un arc 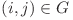$(i, j) \in G$ , atunci i apare înaintea lui j în această ordonare. O astfel de ordonare se poate reprezenta ca o permutare 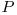$P$ a etichetelor nodurilor grafului $G$ .

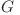Dintre toate sortările topologice ale unui graf, numim sortarea topologică minimă lexicograf acea sortare topolologică a cărei permutare este mai mică lexicografic decât permutarea oricărei alte sortări topologice.

O permutare 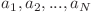$a_1, a_2, ..., a_N$ este mai mică lexicografic decât o altă permutare 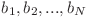$b_1, b_2, ..., b_N$ , dacă există un număr întreg S mai mic sau egal cu N astfel încât 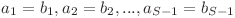$a_1 = b_1, a_2 = b_2, ..., a_{S-1} = b_{S-1}$ , iar $a_S < b_S$ .

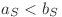Cerinţă

Se dă o permutare 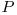$P$ de lungime N. Câte grafuri orientate aciclice etichetate cu primele N numere naturale au proprietatea că 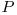$P$ este sortarea lor topologică minimă lexicografic?

Date de intrare

În fişierul dag.in se află pe prima linie numărul N. Pe a doua linie se vor afla N numere distincte cu valori între 1 şi N reprezentând permutarea 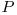$P$ .

Date de ieşire

În fişierul dag.out trebuie să se găsească un singur număr care reprezintă numărul de grafuri orientate aciclice de N noduri pentru care 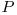$P$ este sortarea lor topologică minimă lexicografic. Deoarece această valoare poate fi foarte mare, se cere să afişaţi doar restul modulo 1.000.000.007 al acesteia.

Restricţii

2 ≤ N ≤ 200.000;
Pentru teste în valoare de 10 puncte, N ≤ 6;
Pentru alte teste în valoare de 55 puncte, N ≤ 2.500.

Exemplu

dag.in	dag.out
3 3 1 2	3
10 1 2 3 5 4 6 7 8 10 9	92960636

Explicaţie

În primul exemplu există 3 grafuri orientate aciclice simple cu 3 noduri a căror sortare topologică minimă este 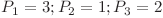$P_1 = 3; P_2 = 1; P_3 = 2$ .

Trebuie sa te autentifici pentru a trimite solutii. Click aici

Cum se trimit solutii?

infoarena informatica de performanta

Dag