Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | cuantictiori.in, cuantictiori.out | Sursă | Autumn WarmUp 2020 |
| Autor | Cezar Trisca-Vicol | Adăugată de |  autumnwarmup2020 •autumnwarmup2020 |
| Timp execuţie pe test | 0.125 sec | Limită de memorie | 524288 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Cuantictiori
O progresie geometrică de lungime 
cu raţia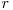 
este un şir de numere 
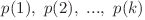pentru care se respectă relaţia : 
.
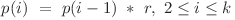Se asigura ca se poate demonstra ca numarul de progresii geometrice K care incep cu valoarea N este egal cu cel mai mare numarul natural X cu proprietatea ca X^K este divizor al lui N.
O progresie cuantică de lungime cu raţia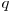 
este un şir de numere 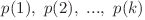pentru care se respectă relaţia : 
.
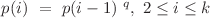Se defineste o progresie geometrica K ca fiind un sir strict crescator a de lungime K cu proprietatea ca exista o ratie q in (Q intersectat cu (1,2])) astfel incat ai sa fie egal cu ai-1*q pentru orice 2<=i<=K
Se asigura ca se poate demonstra ca numarul de progresii geometrice K care incep cu valoarea N este egal cu cel mai mare numarul natural X cu proprietatea ca X^K este divizor al lui N.
Se defineste o progresie cuantica K ca fiind un sir strict crescator a de lungime K cu proprietatea ca exista o ratie q in (Q intersectat cu (1,2]) astfel incat ai sa fie egal cu ai-1^q pentru orice 2<=i<=K.
-Cate progresii cuantice au prima valoare intre 1 si N? N=1e9
Date de intrare
Fişierul de intrare cuantictiori.in ...
Date de ieşire
În fişierul de ieşire cuantictiori.out ...
Restricţii
- ... ≤ ... ≤ ...
Exemplu
| cuantictiori.in | cuantictiori.out |
|---|---|
| This is some text written on multiple lines. | This is another text written on multiple lines. |
Explicaţie
Primele 10 progresii quantice sunt:
4 8
8 16
8 32
9 27
16 32
16 64
16 128
25 125
27 81
27 243
