Fişierul intrare/ieşire:	cmap.in, cmap.out	Sursă	Arhiva educationala
Autor	Arhiva Educationala	Adăugată de	Coroian David •Coroian_David
Timp execuţie pe test	0.2 sec	Limită de memorie	20480 kbytes
Scorul tău	N/A	Dificultate	N/A

Poti vedea testele pentru aceasta problema accesand atasamentele.

Vezi solutiile trimise | Statistici

Cele mai apropiate puncte din plan

Considerăm un plan euclidian ce conţine n puncte date prin coordonatele lor. Distanţa euclidiană dintre două puncte 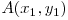şi 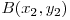se calculează conform formulei: .

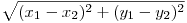Cerinţă

Să se determine distanţa dintre cele mai apropiate două puncte.

Date de intrare

Fişierul de intrare cmap.in conţine pe prima linie un număr n cu semnificaţia din enunţ. Pe următoarele n linii se vor afla câte două numere x_i şi y_i, separate printr-un spaţiu, semnificând coordonatele celui de al i-lea punct.

Date de ieşire

În fişierul de ieşire cmap.out se va afişa distanţa dintre cele mai apropiate două puncte din planul euclidian.

Restricţii

• 1 ≤ n ≤ 100 000.
• -10⁹ ≤ x_i ≤ 10⁹.
• -10⁹ ≤ y_i ≤ 10⁹.
• Oricare două puncte sunt distincte.
• Orice număr se găseşte la coordonate numere întregi.
• Răspunsul va fi considerat corect dacă are o eroare de cel mult 10^-6.
• Pentru 20% din teste 1 ≤ n ≤ 1 000.

Exemplu

Indicaţii de rezolvare

Un algoritm ce consideră fiecare pereche de puncte din cele 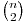are complexitatea O(n²) şi obţine 20 de puncte.

În continuare vom descrie un algoritm divide şi stăpâneşte al cărui timp de execuţie este O(n log₂(n)).

Considerăm P mulţimea tuturor punctelor date. În cazul în care |P| < 3 se vor considera toate cele 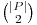perechi de puncte şi se reţine perechea cea mai apropiată. Dacă |P| ≥ 3, se va folosi paradigma divide şi stăpâneşte după cum urmează...

1. Divide: Determină o dreaptă verticală § care împarte mulţimea P, menţionată mai sus, în două submulţimi P_s şi P_d, astfel încât ||P_s| - |P_d|| ≤ 1, adică numărul punctelor din cele două mulţimi diferă cu cel mult unu.
2. Stăpâneşte: Se fac două apeluri recursive, unul pentru a determina cea mai apropiată pereche de puncte din P_s, şi celălalt pentru a determina cea mai apropiată pereche de puncte din P_d. Fie d_s şi d_d valorile returnate şi fie d = min(d_s, d_d).
3. Combină: Cea mai apropiată pereche este cea cu distanţa d, determinată de unul din apelurile recursive, sau este o pereche de puncte cu un punct în P_s şi celălalt în P_d. Observaţi că, dacă există o pereche de puncte cu distanţa mai mică decât d, atunci ambele puncte ale perechii trebuie să fie, daţă de dreapta §, la distanţa maximă d. Astfel, conform desenului alăturat, ambele trebuie să se situeze într-o regiune de lăţime 2d, centrată în jurul dreptei verticale §. Pentru a găsi o astfel de pereche, dacă există, algoritmul urmează paşii...
   • Contruieşte un şir Y care conţine toate punctele ce sunt la o distanţă cel mult d faţă de dreapta verticală §. Şirul este sortat după ordonată.
   • Pentru fiecare punct p din Y, algoritmul încearcă să găsească punctele din Y care sunt la o distanţă de cel mult d unităţi faţă de p. Aşa cum vom arăta mai jos, este necesar să fie considerate doar 7 puncte din Y, care urmează după p. Algoritmul calculează distanţa de la p la fiecare dintre cele 7 puncte şi reţine distanţa d' a parechii celei mai apropiate, găsite dintre toate perechile de puncte din Y.
   • Dacă d' < d, atunci regiunea verficală conţine, într-adevăr, o pereche mai apropiată decât cea care a fost găsită prin apelurile recursive. Se returnează astfel distanţa d'. Altfel, este returnată distanţa d.

O alta soluţie de complexitate O(N*N*log₂N) sortează numerele crescător după abscisa şi apoi foloseşte un algoritm divide et impera. Se împart cele N puncte în doua grupuri st şi dr, se calculează st_min şi dr_min, distanta intre cele mai apropiate puncte din grupul st şi dr, apoi se calculează st_dr_min, distanta intre cele mai apropiate 2 puncte, unul aparţinând grupului st şi altul lui dr. Distanta intre cele mai apropiate puncte o sa fie minim(st_min, dr_min, st_dr_min).

Se observa ca cea mai costisitoare operaţie este cea la care se calculează st_dr_min. Aceasta se poate reduce de la O(N*N) la O(N) folosind următoarea observaţie: notam cu dist minimul dintre st_min si dr_min. Pentru orice punct P din grupul st este suficient sa ne uitam la punctele din dreptunghiul cu laturile dist si 2*dist din grupul dr ca in figura.
Se observa ca în dreptunghi sunt maxim 6 astfel de puncte, deci complexitatea se reduce de la O(N*N) la O(6*N), astfel complexitatea finala devenind O(N*log₂N). Aceasta soluţie foloseşte ideea prezentata mai sus şi obţine 100 de puncte.

Marius: 1. Un evaluator ce compară rezultatele cu o eroare de 10^-6. 2. Ar mai trebui o sursă în O(N^2 log(N)). 3. Sursa ta de 100 de puncte nu e în concordanţă cu explicaţia. Eu zic că faci bine în sursă şi că ar merge explicaţia din CLR. 4. Am mai modificat limita de timp la 1s.

Aplicaţii

1. Harta2

Cum se trimit solutii?