| Fişierul intrare/ieşire: | cmap.in, cmap.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de |  Coroian David •Coroian_David |
| Timp execuţie pe test | 0.2 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Cele mai apropiate puncte din plan
Considerăm un plan euclidian ce conţine n puncte date prin coordonatele lor. Distanţa euclidiană dintre două puncte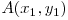 
şi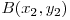 
se calculează conform formulei: 
.
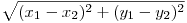Cerinţă
Să se determine distanţa dintre cele mai apropiate două puncte.
Date de intrare
Fişierul de intrare cmap.in conţine pe prima linie un număr n cu semnificaţia din enunţ. Pe următoarele n linii se vor afla câte două numere xi şi yi, separate printr-un spaţiu, semnificând coordonatele punctelor.
Date de ieşire
În fişierul de ieşire cmap.out se va afişa distanţa dintre cele mai apropiate două puncte din planul euclidian.
Restricţii
- 2 ≤ n ≤ 100 000.
- -109 ≤ xi ≤ 109.
- -109 ≤ yi ≤ 109.
- Oricare două puncte sunt distincte.
- Orice număr se găseşte la coordonate numere întregi.
- Răspunsul va fi considerat corect dacă are o eroare de cel mult 10-6.
- Pentru 20% din teste 2 ≤ n ≤ 1 000.
Exemplu
| cmap.in | cmap.out |
|---|---|
| 10 26 77 12 37 14 18 19 96 71 95 91 9 98 43 66 77 2 75 94 91 | 18.681542 |
Indicaţii de rezolvare
În continuare vom descrie un algoritm divide şi stăpâneşte al cărui timp de execuţie este O(n log2(n)).
Considerăm P o submulţime a punctelor date. Iniţial, P va conţine toate punctele. În cazul în care |P| ≤ 3 se vor considera toate cele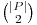 
perechi de puncte şi se reţine perechea cea mai apropiată. Dacă |P| > 3, se va folosi paradigma divide şi stăpâneşte după cum urmează...
- divide: determină o dreaptă verticală d care împarte mulţimea P, menţionată mai sus, în două submulţimi Ps şi Pd, astfel încât ||Ps| - |Pd|| ≤ 1, adică numărul punctelor din cele două mulţimi diferă cu cel mult unu. Punctele din Ps se găsesc în stânga dreptei verticale d iar cele din Pd în dreapta.
- stăpâneşte: se fac două apeluri recursive, unul pentru a determina cea mai apropiată pereche de puncte din Ps, şi celălalt pentru a determina cea mai apropiată pereche de puncte din Pd. Fie §s şi §d valorile returnate şi fie § = min(§s, §d).
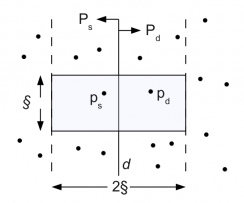
- combină: cea mai apropiată pereche este cea cu distanţa §, determinată de unul din apelurile recursive, sau este o pereche de puncte cu un punct în Ps şi celălalt în Pd. Observaţi că, dacă există o pereche de puncte cu distanţa mai mică decât §, atunci ambele puncte ale perechii trebuie să fie, faţă de dreapta d, la distanţa maximă §. Astfel, conform desenului alăturat, ambele trebuie să se situeze într-o regiune de lăţime 2§, centrată în jurul dreptei verticale d. Pentru a găsi o astfel de pereche, dacă există, algoritmul urmează paşii...
- contruieşte un şir Y care conţine toate punctele ce sunt la o distanţă cel mult § faţă de dreapta verticală d. Şirul este sortat după ordonată.
- pentru fiecare punct p din Y, algoritmul încearcă să găsească punctele din Y care sunt la o distanţă de cel mult § unităţi faţă de p. Aşa cum vom arăta mai jos, este necesar să fie considerate doar 7 puncte din Y, care urmează după p. Algoritmul calculează distanţa de la p la fiecare dintre cele 7 puncte şi reţine distanţa §' a perechii celei mai apropiate, găsite dintre toate perechile de puncte din Y.
- dacă §' < §, atunci regiunea verficală conţine, într-adevăr, o pereche mai apropiată decât cea care a fost găsită prin apelurile recursive. Se returnează astfel distanţa §'. Altfel, este returnată distanţa §.
Corectitudinea
În primul rând, recursivitatea se opreşte când |P| ≤ 3 pentru a evita să împărţim vreodată o mulţime cu un singur punct.
În al doilea rând, să demonstrăm proprietatea conform căreia avem nevoie doar de 7 puncte care urmează după fiecare punct p din şirul Y. Presupunem că la un anumit nivel al recursivităţii, cea mai apropiată pereche de puncte este ps din Ps şi pd din Pd. Astfel, distanţa §' dintre ps şi pd este strict mai mică decât §. Punctul ps trebuie să fie pe dreapta d sau în stânga ei şi la o distanţă mai mică de § unităţi. În mod analog, pd este pe sau în dreapta dreptei d la o distanţă mai mică de § unităţi. Mai mult, ps şi pd se află pe verticală la o distanţă de cel mult § unităţi unul faţă de celălalt. Deci, aşa cum se arată în figura alăturată, cele două puncte se află într-un dreptunghi § x 2§ centrat pe dreapta d.
Arătăm în continuare că cel mult 8 puncte din P se pot găsi în interiorul acestui dreptunghi § x 2§. Studiem pătratul § x § care reprezintă jumătatea stângă a dreptunghiului. Deoarece toate punctele din Ps sunt la o distanţă de cel puţin § unităţi, cel mult 4 puncte se pot situa în interiorul acestui pătrat. În mod analog, cel mult 4 puncte din Pd se pot situa în interiorul pătratului § x § ce reprezintă jumătatea dreaptă a dreptunghiului. Deci, cel mult 8 puncte din P se pot situa în interiorul dreptunghiului § x 2§.
Atunci, presupunând că ps apare cât de devreme este posibil în şirul Y, şi pd cât mai târziu posibil, pd este într-una din cele 7 poziţii care urmează după ps. Deci, am demonstrat corectitudinea algoritmului pentru determinarea perechii celei mai apropiate.
Soluţii
Un algoritm ce consideră fiecare pereche de puncte din cele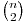 
are complexitatea O(n2) şi obţine 20 de puncte.
În implementare, se va porni de la un şir sortat după abscisă iar în caz de egalitate după ordonată. Şirul se va împărţi în două submulţimi, se va rezolva recursiv fiecare submulţime, iar la revenirea din recursivitate se va obţine şirul Y interclasând cele două subşiruri sortate după ordonată din cele două apeluri recursive. După care se va fixa câte un punct p din Y şi se vor analiza următoarele 7 puncte.
Depinzând de implementare, există soluţie de complexitate O(n log22(n)) şi soluţie de complexitate O(n log2(n)). Soluţia din urmă presupune ca la revenirea din apelul recursiv, cele două submulţimi de puncte sortate după ordonată să fie interclasate în timp liniar şi nu sortate.
