Fişierul intrare/ieşire:	beyond_the_wall.in, beyond_the_wall.out	Sursă	Winter Challenge 2020
Autor	Alexandru Petrescu, Mihai-Cristian Popescu, Tamio-Vesa Nakajima	Adăugată de	Comisia •winterchallenge2020
Timp execuţie pe test	1.15 sec	Limită de memorie	512000 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

Beyond the Wall

Copiii pădurii se feresc de "ceilalţi" aşa că îsî propun să construiască un mare zid pentru a îi ţine la distanţă de restul tărâmului. Se cunoaşte faptul că există puncte în plan care nu au stabilitate aşa că ei doresc să construiască un zid care e cât mai ferit de aceste puncte. Astfel ei şi-au pregătit deja anumite întrebări sub forma "Fiind dată o dreaptă să se răspundă la întrebarea: Câte puncte instabile se află strict sub dreptă?". Deoarece doar tu cunoşti poziţia punctelor şi întrebările lor, ei se pot baza doar pe tine să le răspunzi.

Date de intrare

Fişierul de intrare beyond_the_wall.in conţine pe prima linie numerele N şi Q care reprezintă numărul punctelor instabile, respectiv numărul întrebărilor.
Pe următoarele N linii se vor afla coordonatele punctelor.
Pe următoarele Q linii se vor afla câte două numere M, B care descriu ecuaţia dreptei Y = MX + B

Date de ieşire

În fişierul de ieşire beyond_the_wall.out se vor găsi Q numere, câte unul pe linie, numărul de pe linia i reprezentând răspunsul la întrebarea i.

Restricţii

• Toate numerele din input sunt întregi
• 1 ≤ N ≤ 40000
• -10⁵ ≤ M, B ≤ 10⁵
• 1 ≤ Q ≤ 2 * 10⁵
• 1 ≤ N * Q ≤ 4 * 10⁹
• -10⁵ ≤ X_i, Y_i ≤ 10⁵
• Pentru 5 puncte: 1 ≤ N ≤ 100 şi 1 ≤ Q ≤ 100
• Pentru alte 60 puncte: 1 ≤ N ≤ 5000 şi 1 ≤ N * Q ≤ 4 * 10⁹
• Pentru restul de 35 puncte: Restricţiile iniţiale
• Un punct (X_i, Y_i) se află sub dreapta de ecuaţie Y = MX + B dacă MX_i - Y_i + B > 0

Exemplu

Explicaţie

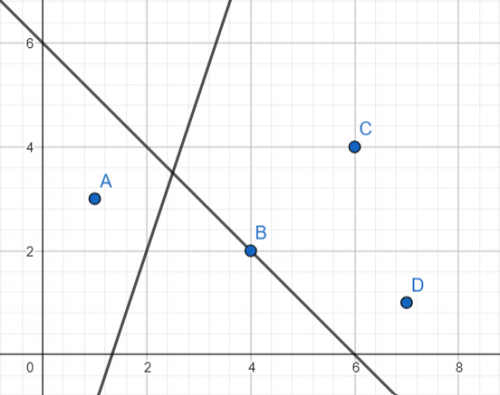
Observăm că pentru prima întrebare punctul B (4, 2) nu este luat în calcul la răspuns deoarece se află pe dreaptă.

Cum se trimit solutii?