Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | arhipelag2.in, arhipelag2.out | Sursă | ONI 2017, clasa a 9-a |
| Autor | Mihai Enache | Adăugată de | |
| Timp execuţie pe test | 0.2 sec | Limită de memorie | 36864 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Arhipelag2
În regiunea Ionia a lumii grece?ti antice, regiune ce corespunde teritoriului actual al M?rii Egee, exist? mai multe insule. Harta m?rii este reprezentat? de o matrice de dimenisuni N x M, având valori de 1 ?i 0, iar fiecare element din matrice reprezint? o zon? de dimensiune 1 × 1 din mare. Liniile matricei sunt numerotate de la 1 la N, de sus în jos, iar coloanele de la 1 la M, de la stânga la dreapta. Astfel, col?ul din stânga sus al matricei este asociat zonei (1, 1), iar col?ul din dreapta jos corespunde zonei (N, M). Un element care con?ine valoarea 0 reprezint? faptul c? în acea zon? se afl? ap?. O insul? este determinat? de un dreptunghi format în totalitate din valori de 1. Se garanteaz? faptul c? toate zonele care con?in valoarea 1 formeaz? dreptunghiuri valide ?i c? oricare dou? insule sunt separate de ap?.
De exemplu, Figura 1 de mai jos reprezint? o hart? valid?, în timp ce Figura 2 ?i Figura 3 NU reprezint? o hart? valid?.
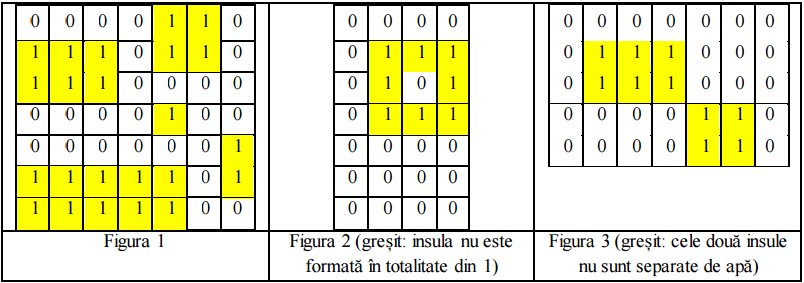
Cerin??
Ionienii, fiind oameni practici, doresc construirea unui far-bibliotec? (a?ezat pe o platform? 1 × 1), într-o zon? acoperit? de ap?. Pozi?ia platformei va fi aleas? într-o celul? C astfel încât suma distan?elor dintre toate insulele ?i C s? fie minim?. Distan?a dintre o celul? C ?i o insul? este definit? ca fiind minimul dintre distan?ele Manhattan dintre C ?i fiecare celul? care apar?ine insulei (distan?a poate trece atât prin alte insule, cât ?i prin zone acoperite de ap?).
Distan?a Manhattan dintre dou? celule aflate pe linia x1 ?i coloana y1, respectiv pe linia x2 ?i coloana y2, este definit? ca |x1 – x2| + |y1 – y2|, unde |x| reprezint? valoarea absolut? a lui x.
Date de intrare
Fi?ierul de intrare arhipelag2.in con?ine, pe prima linie, valorile N ?i M, având semnifica?ia din enun?. Urm?toarele N linii con?in câte M valori binare, separate de câte un spa?iu, reprezentând harta m?rii.
Date de ie?ire
Fi?ierul de ie?ire arhipelag2.out va con?ine o pereche de numere naturale, reprezentând linia si coloana celulei alese de ionieni pentru construc?ie. Dac? exist? mai multe solu?ii posibile, se va alege cea care are linia minim?. Dac? în continuare exist? mai multe solu?ii, se va alege cea care are coloana minim?.
Restric?ii
- Pentru teste în valoare de 15 puncte, 1 <= N, M <= 50
- Pentru alte teste în valoare de 20 de puncte, 1 <= N, M <= 300, iar num?rul de insule din arhipelag nu dep??e?te 300
- Pentru alte teste în valoare de 20 de puncte, 1 <= N, M <= 300
- Pentru restul de teste, 1 <= N, M <= 1000
- Se garanteaz? c? exist? cel pu?in o zon? acoperit? de ap?
Exemplu
| arhipelag2.in | arhipelag2.out | Explica?ie |
|---|---|---|
| 7 7 0 1 0 1 0 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 0 1 1 | 2 3 | Notând cu D(x1, y1, x2, y2) insula determinat? de dreptunghiul având col?ul stânga sus în (x1, y1) ?i col?ul dreapta jos în (x2, y2), arhipelagul con?ine urm?toarele insule: D1, D2, D3, D4 ?i D5. Notând cu dist(D) distan?a dintre celula (2, 3) ?i insula D, distan?ele sunt urm?toarele: dist(D1) = min(|2 – 1| + |3 – 2|, |2 – 2| + |3 - 2|) = 1, dist(D2) = 1, dist(D3) = 3, dist(D4) = 5 ?i dist(D5) = 7. |
| 4 4 0 0 1 1 0 0 1 1 0 0 1 1 0 0 0 0 | 1 2 | Pentru fiecare dintre celulele (1, 2), (2, 2), (3, 2), (4, 3) si (4, 4), distan?a dintre celul? ?i singura insul? existent? în acest exemplu este aceea?i. Se va alege cea care are linia minim?, iar în caz de egalitate se va alege cea care are coloana minim?. Astfel, celula (1, 2) reprezint? solu?ia. |
