Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | inversmodular.in, inversmodular.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de | |
| Timp execuţie pe test | 0.025 sec | Limită de memorie | 5120 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Invers modular
Se da un graf bidirectionat G cu N noduri si M muchii cu cost. Se cere sa se aleaga o submultime de muchii dintre aceste M, de cost minim, astfel incat sa existe un singur drum intre oricare doua noduri parcurgand doar muchii din submultimea aleasa.
Date de intrare
Fisierul de intrare apm.in va contine pe prima linie numerele N si M, separate printr-un spatiu.Pe urmatoarele M randuri se vor gasi muchiile sub forma X, Y,$C$, cu semnificatia exista muchie intre X si Y cu costul C.
Date de ieşire
Fisierul de iesire apm.out va contine pe prima linie costul total minim.
Restricţii
- 1 ≤ N ≤ 200.000
- 1 ≤ M ≤ 200.000
- Pentru 20% din teste N,M ≤ 20
- Pentru inca 30% din teste N,M ≤ 5.000
- Intre oricare doua noduri va exista decat o muchie.
Exemplu
| inversmodular.in | inversmodular.out |
|---|---|
| 9 14 1 2 10 1 3 -11 2 4 11 2 5 11 5 6 13 3 4 10 4 6 12 4 7 5 3 7 4 3 8 5 8 7 5 8 9 4 9 7 3 6 7 11 | 3 |
Explicaţie
5 * 3 este congruent cu 1, modulo 7, deoarece restul impartirii lui 15 la 7 este 1.
Indicaţii de rezolvare
Un algoritm evident ar fi incercarea tuturor numerelor X intre 1 si N-1 si verificarea proprietatii din enunt pentru X. O astfel de solutie are complexitatea O(N) si obtine 30 de puncte. Sursa se poate gasi aici.
O complexitate mai buna se obtine folosind teorema lui Euler, din care avem ca 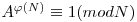 , unde
, unde 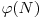 reprezinta numarul numerelor mai mici decat N si prime cu N. Cum
reprezinta numarul numerelor mai mici decat N si prime cu N. Cum 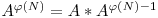 rezulta ca
rezulta ca 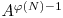 este inversul modular al lui A. Solutia problemei va fi deci
este inversul modular al lui A. Solutia problemei va fi deci 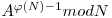 . Putem folosi exponentierea in timp logaritmic pentru a calcula aceasta putere in complexitate O(log2N). In plus, putem calcula
. Putem folosi exponentierea in timp logaritmic pentru a calcula aceasta putere in complexitate O(log2N). In plus, putem calcula 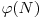 in complexitate
in complexitate 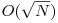 . Pentru cazul particular cand N este prim,
. Pentru cazul particular cand N este prim, 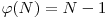 , deci raspunsul va fi AN-2 (dupa cum reiese si din mica teorema a lui Fermat). O implementare ce se bazeaza pe aceasta idee se gaseste aici.
, deci raspunsul va fi AN-2 (dupa cum reiese si din mica teorema a lui Fermat). O implementare ce se bazeaza pe aceasta idee se gaseste aici.
Complexitatea optima pentru determinarea inversului modular este O(log2N). Putem folosi principiul extins al lui Euclid: oricare ar fi A si N numere intregi exista doua numere X si Y de asemenea intregi astfel incat A * X + N * Y = cmmdc(A, N). Cum in problema determinarii inversului modular avem cmmdc(A, N) = 1, exista X si Y astfel incat A * X + N * Y = 1. Considerand ecuatia modulo N, deoarece N * Y este divizibil cu N, avem A * X congruent cu 1 (modulo N), deci X este inversul modular pentru A. Coeficientii X si Y pot fi determinati in timp logaritmic. X poate sa fie si negativ, deci trebuie sa adaugam N la X pana cand devine pozitiv. O astfel de solutie se poate gasi aici.
Aplicatii
O aplicatie foarte utila a inversilor modulari este calcularea combinarilor, modulo un numar prim P dat. De exemplu, avem:
![C^K_N = \frac{N!}{K!*(N-K)!} = N! * (K!)^{-1} * [(N-K)!]^{-1} C^K_N = \frac{N!}{K!*(N-K)!} = N! * (K!)^{-1} * [(N-K)!]^{-1}](http://www.infoarena.ro/static/images/latex/a27dfb7d6132b948f8d95c4f9a23acbc_6.19841pt.gif)
Prin 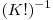 si
si ![[(N-K)!]^{-1} [(N-K)!]^{-1}](http://www.infoarena.ro/static/images/latex/cae953223577328360191dea08b2a3cf_3.5pt.gif) se inteleg inversii modulari ai acestor numere, modulo P. Astfel putem calcula o combinare de ordin N, modulo P, in timp O(N).
se inteleg inversii modulari ai acestor numere, modulo P. Astfel putem calcula o combinare de ordin N, modulo P, in timp O(N).
Alte aplicatii ce folosesc notiunile prezentate mai sus se regasesc in urmatoarele probleme:
 Poti vedea testele pentru aceasta problema accesand
Poti vedea testele pentru aceasta problema accesand 