| Fişierul intrare/ieşire: | admitere-fmi-2016.in, admitere-fmi-2016.out | Sursă | Admitere FMI 2016 |
| Autor | Adăugată de | ||
| Timp execuţie pe test | 0.25 sec | Limită de memorie | 16384 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Admitere FMI 2016
 Versiunea originală a acestei probleme a fost propusă în cadrul examenului de admitere al Facultăţii de Matematică şi Informatică, Universitatea din Bucureşti. Versiunea originală a acestei probleme a fost propusă în cadrul examenului de admitere al Facultăţii de Matematică şi Informatică, Universitatea din Bucureşti.Versiunea de faţă este publicată cu permisiunea organizatorilor examenului, dar aceştia nu sunt responsabili pentru modificările aduse problemei în scopul adaptării la contextul evaluării automate. Rezolvarea acestei probleme poate diferi substanţial de experienţa examenului real. În particular, punctajul obţinut pe această problemă nu poate fi corelat cu notarea oficială. Informaţii oficiale despre examenul de admitere al Facultăţii de Matematică şi Informatică, cât şi despre pregătiri oficiale pentru examen se pot găsi aici. |
Ionuţ tocmai a terminat liceul şi susţine examenul de admitere la facultate. Ştiind că s-a pregătit foarte bine pentru examen, el doreşte să îşi anunţe reuşita după examen printr-o postare pe Facebook. Ionuţ cunoaşte n utilizatori reprezentaţi de numerele de la 1 la n, între care există m relaţii de prietenie de forma i j, unde i şi j sunt utilizatori, iar n şi m sunt numere naturale nenule. Un utilizator nu poate fi prieten cu el însuşi, iar o relaţie de prietenie între doi utilizatori ne spune că fiecare dintre ei este prieten cu celălalt.
Întrucât doreşte ca postarea lui să fie cât mai răspândită, Ionuţ vrea să afle care sunt utilizatorii cei mai bine conectaţi din mulţimea sa de cunoscuţi, pentru ca eventual să le ceară prietenia. Pentru aceasta, Ionuţ trebuie să găsească cea mai mare submulţime de utilizatori cunoscuţi, în care fiecare utilizator din această submulţime are cel puţin k prieteni aflaţi la rândul lor în submulţime, unde k este un număr natural nenul.
Ajutaţi-l pe Ionuţ să găsească o soluţie la problema sa, rezolvând următoarele subpuncte:
a) Să se determine şi să se afişeze, în ordine de la 1 la n, numărul de prieteni al fiecăruia dintre cei n utilizatori, conform relaţiilor de prietenie date.
b) Să se determine şi să se afişeze, printr-o soluţie de complexitate timp cât mai bună, în funcţie de datele de intrare, membrii celei mai mari submulţimi de utilizatori, cu proprietatea că fiecare utilizator din această submulţime are cel puţin k prieteni aflaţi la rândul lor în submulţime. În cazul în care nu există o astfel de submulţime pentru k dat, răspunsul va fi cuvântul NU.
Date de intrare
Fişierul de intrare admitere-fmi-2016.in conţine numerele n, m şi k, pe aceeaşi linie, separate prin spaţiu, precum şi 2m numere naturale cuprinse între 1 şi n, pe o linie nouă, separate prin spaţiu, reprezentând în ordine cele m relaţii de prietenie între cei n utilizatori.
Date de ieşire
Prima linie a fişierului admitere-fmi-2016.out conţine n numere, reprezentând numărul de prieteni al fiecăruia dintre cei n utilizatori.
Pe următoarea linie se află numere separate prin spaţiu, reprezentând utilizatorii din submulţimea cerută, sau şirul NU în caz că aceasta nu există.
Restricţii
- 1 ≤ n ≤ 100.000
- 1 ≤ m ≤ 200.000
- 1 ≤ k < n
- Nu se iau în considerare submulţimile formate dintr-un singur utilizator cu k prieteni.
Exemplu
| admitere-fmi-2016.in | admitere-fmi-2016.out |
|---|---|
| 5 5 2 1 2 5 1 3 2 4 5 1 4 | 3 2 1 2 2 1 4 5 |
| 5 5 3 1 2 5 1 3 2 4 5 1 4 | 3 2 1 2 2 NU |
| 11 18 3 1 8 4 7 7 10 11 10 2 1 2 3 8 9 8 3 9 3 9 2 5 6 5 11 1 4 10 6 7 6 2 8 11 7 11 6 | 3 4 3 2 2 4 4 4 3 3 4 2 3 6 7 8 9 10 11 |
Explicaţie
Pe primul exemplu avem o mulţime formată din 5 cunoscuţi. Utilizatorii 1, 4 şi 5 formează o submulţime cu proprietatea cerută:
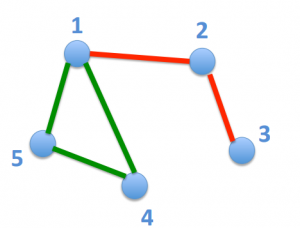
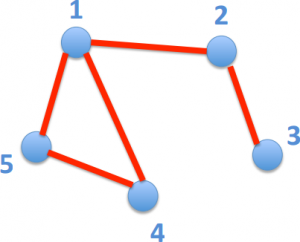
Pe al doilea exemplu avem aceleaşi relaţii de prietenie, dar 1 este singurul care are cel puţin alţi trei prieteni:
Pe al treilea exemplu avem situaţia reprezentată mai jos: