| Fişierul intrare/ieşire: | ace.in, ace.out | Sursă | OJI 2017, clasa a 9-a |
| Autor | Octavian Dumitrascu | Adăugată de | |
| Timp execuţie pe test | 0.25 sec | Limită de memorie | 36864 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Ace
Pe o zonă în formă de dreptunghi cu laturile de lungimi N şi M se găsesc NxM pătrate de latură 1. În centrul fiecărui pătrat se găseşte înfipt câte un ac de grosime neglijabilă. Fiecare ac este descris de înălţimea sa. Această zonă se poate reprezenta ca un tablou bidimensional de dimensiuni N şi M, iar fiecare element din matrice reprezintă înălţimea (număr natural nenul) fiecărui ac. În centrul pătratului (N, M) există o cameră de luat vederi de ultimă generaţie, mobilă, care se poate roti cu 360° în orice plan, situată la nivelul solului. Dimensiunile camerei sunt neglijabile. De exemplu, dacă avem zona sub forma:
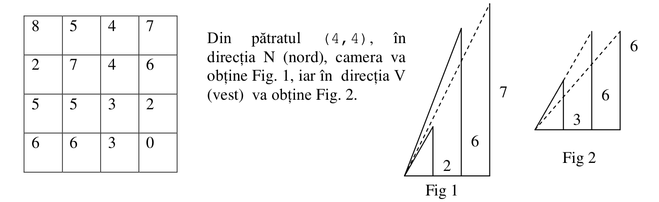
Pentru direcţia N, camera va vedea acul de coordonatele (3,4) – în totalitate, iar acul (2,4) se va vedea doar parţial. Acul (1,4) nu se vede pentru că este acoperit total de (2,4). În direcţia V, camera va vedea doar acul (4,3), deoarece (4,2) şi (4,1) sunt acoperite total de (4,3). Pentru celelalte direcţii se vor vedea parţial sau în totalitate acele (3,3), (3,2), (3,1), (2,3), (1,3), (2,2), (2,1), (1,2). Acul (1,1) nu se vede din cauza acului (2,2), care îl acoperă total. Acul (2,2) se vede doar parţial, pentru că o parte din el este acoperit de acul (3,3).
Cerinţe
- Câte ace vede camera de luat vederi dacă se poate roti în plan vertical, doar în direcţiile N şi V?
- Câte ace vede camera de luat vederi dacă se poate roti în orice plan şi în orice direcţii?
Date de intrare
Fişierul de intrare ace.in conţine pe prima linie numărul P care poate fi 1 sau 2, pentru prima, respectiv a doua cerinţă.
Pe a doua linie se găsesc numerele N, M reprezentând dimensiunile tabloului, apoi pe următoarele N linii câte M numere naturale, despărţite prin câte un spaţiu, reprezentând înălţimile acelor.
Date de ieşire
Fişierul de ieşire ace.out va conţine pe prima linie numărul de ace văzute pentru cerinţă indicată de valoarea numărului P.
Restricţii
- 2 ≤ N ≤ 1000
- 2 ≤ M ≤ 1000
- Elementele matricei sunt numere naturale nenule mai mici decât 1000, cu excepţia numărului de pe linia N şi coloana M care este 0.
- Pentru rezolvarea corectă a cerinţei 1 se acordă 20 puncte, pentru rezolvarea corectă a cerinţei 2 se acordă 70 de puncte, iar din oficiu se acordă 10 de puncte.
- Pentru cerinţa 2 există teste în valoare de 20 puncte cu N,M ≤ 50.
- Pentru cerinţa 2 există teste în valoare de 45 puncte cu N,M ≤ 100.
Exemplu
| ace.in | ace.out | Explicaţie |
|---|---|---|
| 1 4 4 8 5 4 7 2 7 4 6 5 5 3 2 6 6 3 0 | 3 | Pentru cerinţa 1 avem direcţiile N şi V: Pentru direcţia N, camera va vedea acul de coordonatele (3,4) – în totalitate, iar acul (2,4) se va vedea doar parţial. Acul (1,4) nu se va vedea pentru că este acoperit total de (2,4). În direcţia V, camera va vedea doar acul (4,3), deoarece acele (4,2) şi (4,1) sunt acoperite total de acul (4,3). |
| 2 4 4 8 5 4 7 2 7 4 6 5 5 3 2 6 6 3 0 | 11 | Pentru cerinţa 2 camera va vedea cele 3 ace din direcţiile N şi V (vezi mai sus) şi 8 pentru celelalte direcţii se vor vedea parţial sau în totalitate acele (3,3), (3,2), (3,1), (2,3), (1,3), (2,2), (2,1), (1,2). Acul (1,1) nu se vede din cauza celui de pe (2,2) care il acoperă total. Acul (2,2) se vede doar parţial, pentru că o parte din el este acoperit de acul (3,3). |
| 2 4 3 5 4 7 6 4 6 5 3 2 6 3 0 | 8 | Pentru cerinţa 2 camera va vedea în N (3,3), (2,3), în V va vedea (4,2). În celelalte direcţii camera va vedea parţial sau în totalitate acele (3,2), (3,1), (2,2), (1,2), (1,1). |
