Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2009-12-02 17:39:00.
Revizia anterioară   Revizia următoare  

 

Fişierul intrare/ieşire:2sat.in, 2sat.outSursăArhiva Educationala
AutorArhiva EducationalaAdăugată deCezarMocanCezar Mocan •CezarMocan
Timp execuţie pe test0.425 secLimită de memorie65536 kbytes
Scorul tăuN/ADificultateN/A

Vezi solutiile trimise | Statistici

2SAT

Problema satisfiabilităţii, notată prescurtat cu SAT cere determinarea existenţei unei atribuiri satisfiabile pentru o formulă booleană. O atribuire de valori booleene pentru variabilele acestei expresii se numeşte atribuire satisfiabilă dacă evaluarea expresiei după atribuirea valorilor are ca rezultat valoarea de adevăr adevărat.

Un exemplu de formulă ar fi: 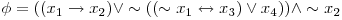\phi = ((x_{1} \rightarrow x_{2}) \vee \sim((\sim x_{1} \leftrightarrow x_{3}) \vee x_{4})) \wedge \sim x_{2} , aceasta având o atribuire satisfiabilă \langle x_{1} = 0, x_{2} = 0, x_{3} = 1, x_{4} = 1 \rangle .

Orice formulă booleană poate fi transformată în două forme:

  • în forma normal conjunctivă expresia este scrisă ca o conjuncţie de propoziţii, iar fiecare propoziţie este o disjuncţie de literali;
  • în forma normal disjunctivă expresia este scrisă ca o disjuncţie de propoziţii în interiorul cărora există doar conjuncţii de literali;

În rezolvarea acestei probleme ne interesează doar forma normal conjunctivă. Problema SAT pe cazul general este NP-completă, chiar şi dacă restricţionăm expresiile la unele care în forma normal conjunctivă au doar trei literali în fiecare dintre propoziţii. Problema satisfiabilităţii pentru asemenea expresii se numeşte 3SAT.

În continuare ne vom ocupa de problema 2SAT, ce are doi literali în fiecare din propoziţiile ce alcătuiesc forma normal conjunctivă, 2SAT fiind rezolvabilă în timp polinomial. Un exemplu de o astfel de expresie: 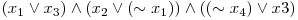(x_{1} \vee x_{3}) \wedge (x_{2} \vee (\sim x_{1})) \wedge ((\sim x_{4}) \vee x{3}) .

Cerinţă

Dandu-se o expresie 2SAT sa se determine o atribuire satisfiabila a acesteia.

Date de intrare

Fişierul de intrare 2sat.in va contine pe prima linie 2 numere naturale, N - numarul de termeni care apar in expresie si M - numarul de propozitii disjunctive din care este formata expresia. Pe fiecare dintre urmatoarele M linii se vor afla cate 2 numere intregi, numerele de ordine ale termenilor prezenti in fiecare dintre propozitii. Semnul - in fata unui numar reprezinta ca termenul respectiv apare negat in expresie.

Date de ieşire

În fişierul de ieşire 2sat.out se vor afisa N numere naturale, 0 sau 1, reprezentand o atribuire satisfiabila pentru expresia data in fisierul de intrare.

Restricţii

  • 1 ≤ N ≤ 100000
  • 1 ≤ M ≤ 100000

Exemplu

2sat.in2sat.out
4 5
1 -2
-1 -3
1 2
4 -3
4 -1
1 0 0 1

Indicatii pentru rezolvare

O solutie evidenta este incercarea celor 2N configuratii posibile pentru termenii expresiei si apoi verificarea lor, aceasta abordare ducand la o complexitate de O(2N * M). Cu aceasta complexitate se obtin 20 de puncte, iar o sursa demonstrativa se gaseste aici.

Următoarea soluţie pare trivială, dar găsirea acestui algoritm şi realizarea faptului că el rezolvă corect problema sunt mai grele decât impresia lăsată după citirea ei. Considerăm o propoziţie oarecare cu două variabile p şi q, apoi una dintre ele, de exemplu p. Ii atribuim lui p valoarea 0. Pentru ca propoziţia respectivă să aibă 1 valoarea de adevăr, atunci valoarea lui q trebuie fixată. Fixând si valoarea lui q, probabil si alte propoziţii ce conţin literalul q vor avea celălalt literal fixat. Propagăm astfel o serie de schimbări. După ce toate schimbările forţate au fost făcute, propoziţiile rezultate vor fi de următoarele tipuri: A SAU B, 1 SAU 0, 1 SAU 1, 1 SAU B. Propozitii de tipul 0 SAU B nu pot aparea, pentru ca toate schimbarile fortate au fost deja propagate. Dacă apare o propoziţie 0 SAU 0 atunci alegerea făcută pentru valoarea lui p este greşită. Vom încerca şi alegerea opusă pentru p. Dacă ambele duc la o propoziţie de tip atunci expresia nu poate fi satisfăcută. Propoziţiile de forma 1 SAU 0, 1 SAU 1, 1 SAU B pot fi ignorate. În acest fel am eliminat cel puţin o variabilă şi o propoziţie din expresie. Dacă expresia iniţială era satisfiabilă, atunci şi expresia din care s-au eliminat câteva propoziţii a rămas satisfiabilă. Continuând pe această idee obţinem un algoritm de complexitate O(N * M), pentru că la fiecare atribuire de valoare pentru o variabilă parcurgem şirul de propoziţii o dată. Aceasta solutie trebuie sa obtina 40 de puncte, sursa se gaseste aici.

O alta solutie neoptima, in complexitatea O(N2) se bazeaza pe un algoritm randomizat. Initial se atribuie valori arbitrare variabilelor, iar apoi cat timp expresia nu este satisfacuta se gaseste o propozitie cu valoarea de adevar 0 si se schimba valoarea unuia dintre cei 2 termeni componenti ai propozitiei. Pentru o demonstratie a functionalitatii acestui algoritm consultati articolul

//TODO: Solutia in O(M + N)

Marius Cezar, scuze că îţi zic puţin târziu, dar, din punctul meu de vedere nu mai e nevoie să explici în detaliu soluţiile. Sunt deja prezentate în articolul lui Cosmin. Câte cuvinte despre fiecare (cum e la ultima cu algoritmul randomizat) şi o sursă beton sunt de ajuns. Dar să fie beton sursa. :)

Aplicatii

Trebuie sa te autentifici pentru a trimite solutii. Click aici

Cum se trimit solutii?