Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2009-06-30 19:41:29.
Revizia anterioară   Revizia următoare  

1. Arii

Noţiunea de arie este una de bază în geometria analitică. Este necesară însă o prezentare a diferitelor metode de a calcula ariile in contextul prelucrarii datelor pe calculator.

Aria unui triunghi

În determinarea ariei unui triunghi se poate folosi formula lui Heron:
\begin{math} A=\sqrt{s\cdot(s-a)\cdot(s-b)\cdot(s-c)}\end
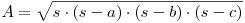
În formulă, s reprezintă semiperimetrul triunghiului, iar a, b, c laturile triunghiului. Această formulă apare şi într-o altă formă, mult mai adecvată algoritmilor prin faptul că se evită calcularea lungimii laturilor cu radical:
\begin{math} A=\frac{1}{4}\sqrt{4a^{2}b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}\end

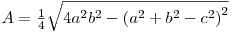
În contextul geometriei vectoriale, modulul produsului vectorial a doi vectori o reprezintă aria paralelogramului cuprins între vectori. Aplicând raţionamentul la triunghiuri, obţinem relaţia:
\begin{math} A = \frac{1}{2}\|\vec{v}\times\vec{w}\| = \frac{1}{2}\cdot abs\left(\left|\begin{array}{ccc} \ x_1 & y_1 & 1\ x_2 & y_2 & 1\ x_3 & y_3 & 1\end{array}\right|\right)\end{math}

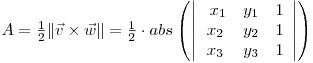
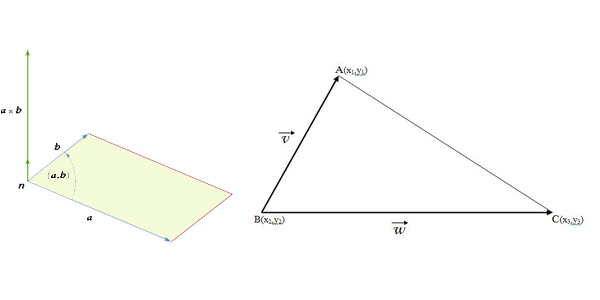
Aria unui poligon

Aria unui poligon convex cu n laturi o putem calcula foarte usor folosind formula pentru aria unui triunghi astfel.

\displaystyle \sum_{i=2}^{i<n} Arie(p_{1},p_{i},p_{i+1})

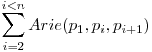
Unde 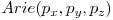Arie(p_{x},p_{y},p_{z}) reprezinta aria triunghiului determinat de punctele px, py, pz.

Aria unui poligon concav se calculeaza la fel doar ca atunci cand calculam 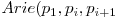Arie(p_{1},p_{i},p_{i+1} renuntam la abs, si tinem minte semnul determinantului si luam valoarea absoluta dupa ce am calculat intreaga suma.