Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2009-06-28 22:36:19.
Revizia anterioară   Revizia următoare  

Aria unui triunghi

Aria unui triunghi determinat de punctele A(x1,y1), B(x2,y2) si C(x3,y3) este egala cu :

A = \frac{1}{2} * abs \left( \left| \begin{array}{ccc} \ x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1\end{array} \right| \right)

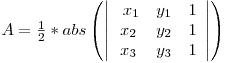
Unde abs(x) reprezinta valoarea absoluta a lui x. Determinantul de mai sus poate fi folosit si pentru a vedea daca cele 3 puncte sunt in sens invers sau direct trigonometric, el fiind negativ in cazul in care punctele sunt in sens invers trigonometric.

Aria unui poligon

Aria unui poligon convex cu n laturi o putem calcula foarte usor folosind formula pentru aria unui triunghi astfel.

\displaystyle \sum_{i=2}^{i<n} Arie(p_{1},p_{i},p_{i+1})

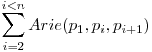
Unde 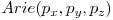Arie(p_{x},p_{y},p_{z}) reprezinta aria triunghiului determinat de punctele px, py, pz.

Aria unui poligon concav se calculeaza la fel doar ca atunci cand calculam 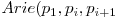Arie(p_{1},p_{i},p_{i+1} renuntam la abs, si tinem minte semnul determinantului si luam valoarea absoluta dupa ce am calculat intreaga suma.