Lucrul cu numere mari

De multe ori, in probleme, apar situatii cand este nevoie sa memoram numere intregi foarte mari (de ordinul sutelor de cifre), iar uneori trebuie sa efectuam si operatii aritmetice cu aceste numere.

Numerele reprezentate pe vectori le vom numi pur si simplu "vectori", iar numerele reprezentate printr-un tip ordinal de date le vom numi, printr-o analogie usor fortata cu matematica, "scalari". Sa vedem acum cum se efectueaza operatiile elementare pe aceste numere.

Initializarea

Un vector poate fi initializat in trei feluri: cu 0, cu un scalar sau cu un alt vector.

La initializarea cu 0, singurul lucru pe care il avem de facut este sa setam numarul de cifre pe 0. De aceea, este practic inutil sa implementam aceasta functie ca atare; putem folosi in loc singura instructiune pe care ea o contine.

void Atrib0(Huge H) {
  H[0] = 0;
}

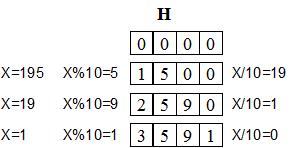
La initializarea cu un scalar nenul, trebuie sa asezam fiecare cifra pe pozitia corespunzatoare, afland in paralel si numarul de cifre. Se incepe cu cifra unitatilor, si la fiecare pas se pune in vector cifra cea mai putin semnificativa, dupa care numarul de reprezentat se imparte la 10 (neglijandu-se restul), iar numarul de cifre se incrementeaza.

void AtribValue(Huge H, unsigned long X) {
  H[0] = 0;
  while (X) {
      ++H[0];
      H[H[0]] = X % BASE;
      X /= BASE;
  }
}

Iata, de exemplu, cum se pune pe vector numarul 195:

In sfarsit, initializarea unui vector cu altul se face printr-o simpla copiere (se pot folosi cu succes rutine de lucru cu memoria, cum ar fi FillChar in Pascal sau memmove in C). Pentru eleganta, poate fi folosita si atribuirea cifra cu cifra:

void AtribHuge(Huge H, Huge X) {
  int i;
  for (i = 0; i <= X[0]; ++i) {
    H[i] = X[i];
  }
}

Compararea

Pentru a compara doua numere "uriase", incepem prin a afla numarul de cifre semnificative (deoarece, in urma anumitor operatii pot rezulta zerouri nesemnificative care "atarna" totusi la numarul de cifre). Aceasta se face decrementand numarul de cifre al fiecarui numar atata timp cat cifra cea mai semnificativa este 0. Dupa ce ne-am asigurat asupra acestui punct, comparam numarul de cifre al celor doua cifre. Numarul cu mai multe cifre este cel mai mare. Daca ambele numere au acelasi numar de cifre, pornim de la cifra cea mai semnificativa si comparam cifrele celor doua numere pana la prima diferenta intalnita. In acest moment, numarul a carui cifra este mai mare este el insusi mai mare.
Daca toate cifrele numerelor sunt egale doua cate doua, atunci in mod evident numerele sunt egale.

Dupa cum se vede, algoritmul seamana foarte bine cu ceea ce s-a invatat la matematica prin clasa a II-a (doar ca atunci nu ni s-a spus ca este vorba de un "algoritm"). Rutina de mai jos compara doua numere uriase H1 si H2 si intoarce -1, 0 sau 1, dupa H1 este mai mic, egal sau mai mare decat H2.

int Sgn(Huge H1, Huge H2) {
  // Elimina zero-urile semnificative, daca exista.
  while (H1[0] && !H1[H1[0]]) H1[0]--;
  while (H2[0] && !H2[H2[0]]) H2[0]--;

  if (H1[0] < H2[0]) {
    return -1;
  } else if (H1[0] > H2[0]) {
    return +1;
  }

  for (int i = H1[0]; i > 0; --i) {
    if (H1[i] < H2[i]) {
      return -1;
    } else if (H1[i] > H2[i]) {
      return +1;
    }
  }
  return 0;
}

Adunarea a doi vectori

Fiind dati doi vectori, A cu M cifre si B cu N cifre, adunarea lor se face in mod obisnuit, ca la aritmetica. Pentru a evita testele de depasire, se recomanda sa se completeze mai intai vectorul cu mai putine cifre cu zerouri pana la dimensiunea vectorului mai mare. La sfarsit, vectorul suma va avea dimensiunea vectorului mai mare dintre A si B, sau cu 1 mai mult daca apare transport de la cifra cea mai semnificativa. Procedura de mai jos adauga numarul B la numarul A.

void Add(Huge A, Huge B)
/* A <- A+B */
{ int i,T=0;

  if (B[0]>A[0])
    { for (i=A[0]+1;i<=B[0];) A[i++]=0;
      A[0]=B[0];
    }
    else for (i=B[0]+1;i<=A[0];) B[i++]=0;
  for (i=1;i<=A[0];i++)
    { A[i]+=B[i]+T;
      T=A[i]/10;
      A[i]%=10;
    }
  if (T) A[++A[0]]=T;
}

Scaderea a doi vectori

Se dau doi vectori A si B si se cere sa se calculeze diferenta A - B. Se presupune B ≤ A (acest lucru se poate testa cu functia Sgn). Pentru aceasta, se porneste de la cifra unitatilor si se memoreaza la fiecare pas "imprumutul" care trebuie efectuat de la cifra de ordin imediat superior (imprumutul poate fi doar 0 sau 1). Deoarece B ≤ A, avem garantia ca pentru a scadea cifra cea mai semnificativa a lui B din cifra cea mai semnificativa a lui A nu e nevoie de imprumut.

void Subtract(Huge A, Huge B)
/* A <- A-B */
{ int i, T=0;

  for (i=B[0]+1;i<=A[0];) B[i++]=0;
  for (i=1;i<=A[0];i++)
    A[i]+= (T=(A[i]-=B[i]+T)<0) ? 10 : 0;
    /* Adica A[i]=A[i]-(B[i]+T);
       if (A[i]<0) T=1; else T=0;
       if (T) A[i]+=10; */
  while (!A[A[0]]&&A[0]>1) A[0]--;
}

Inmultirea si impartirea cu puteri ale lui 10

Aceste functii sunt uneori utile. Ele pot folosi si functiile de inmultire a unui vector cu un scalar, care vor fi prezentate mai jos, dar se pot face si prin deplasarea intregului numar spre stanga sau spre dreapta. De exemplu, inmultirea unui numar cu 100 presupune deplasarea lui cu doua pozitii inspre cifra cea mai semnificativa si adaugarea a doua zerouri la coada. Principalul avantaj al scrierii unor functii separate pentru inmultirea cu 10, 100, ..., este ca se pot folosi rutinele de acces direct al memoriei (FillChar, respectiv memmove). Iata functiile care realizeaza deplasarea vectorilor, atat prin mutarea blocurilor de memorie, cat si prin atribuiri succesive.

void Shl(Huge H, int Count)
/* H <- H*10ACount */
{ 
  /* Shifteaza vectorul cu Count pozitii */
  memmove(&H[Count+1],&H[1],sizeof(int)*H[0]);
  /* Umple primele Count pozitii cu 0 */
  memset(&H[1],0,sizeof(int)*Count);
  /* Incrementeaza numarul de cifre */
  H[0]+=Count;
}

void Shl2(Huge H, int Count)
/* H <- H*10ACount */
{ int i;

  /* Shifteaza vectorul cu Count pozitii */
  for (i=H[0];i;i--) H[i+Count]=H[i];
  /* Umple primele Count pozitii cu 0 */
  for (i=1;i<=Count;) H[i++]=0;
  /* Incrementeaza numarul de cifre */
  H[0]+=Count;
}

void Shr(Huge H, int Count)
/* H <- H/10ACount */
{ 
  /* Shifteaza vectorul cu Count pozitii */
  memmove(&H[1],&H[Count+1],sizeof(int)*(H[0]-Count));
  /* Decrementeaza numarul de cifre */
  H[0]-=Count;
}

void Shr2(Huge H, int Count)
/* H <- H/10ACount */
{ int i;

  /* Shifteaza vectorul cu Count pozitii */
  for (i=Count+1;i<=H[0];i++) H[i-Count]=H[i];
  /* Decrementeaza numarul de cifre */
  H[0]-=Count;
}

Inmultirea unui vector cu un scalar

Si aceasta operatie este o simpla implementare a modului manual de efectuare a calculului. La inmultirea "de mana" a unui numar mare cu unul de o singura cifra, noi parcurgem deinmultitul de la sfarsit la inceput, si pentru fiecare cifra efectuam urmatoarele operatii:

Inmultim cifra respectiva cu inmultitorul;
Adaugam "transportul" de la inmultirea precedenta;
Separam ultima cifra a rezultatului si o trecem la produs;
Celelalte cifre are rezultatului constituie transportul pentru urmatoarea inmultire;
La sfarsitul inmultirii, daca exista transport, acesta are o singura cifra, care se scrie inaintea rezultatului.

Exact acelasi procedeu se poate aplica si daca inmultitorul are mai mult de o cifra. Singura deosebire este ca transportul poate avea mai multe cifre (poate fi mai mare ca 9). Din aceasta cauza, la sfarsitul inmultirii, poate ramane un transport de mai multe cifre, care se vor scrie inaintea rezultatului. Iata de exemplu cum se calculeaza produsul 312 x 87:

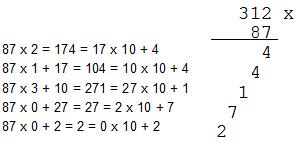
Procedura este descrisa mai jos:

void Mult(Huge H, unsigned long X)
/* H <- H*X */
{ int i;
  unsigned long T=0;

  for (i=1;i<=H[0];i++)
    { H[i]=H[i]*X+T;
      T=H[i]/10;
      H[i]=H[i]%10;
    }
  while (T) /* Cat timp exista transport */
    { H[++H[0]]=T%10;
      T/=10;
    }
}

Inmultirea a doi vectori

Daca ambele numere au dimensiuni mari si se reprezinta pe tipul de date Huge, produsul lor se calculeaza inmultind fiecare cifra a deinmultitului cu fiecare cifra a inmultitorului si trecand rezultatul la ordinul de marime (exponentul lui 10) cuvenit. De fapt, acelasi lucru il facem si noi pe hartie. Considerand acelasi exemplu, in care ambele numere sunt "uriase", produsul lor se calculeaza de mana astfel

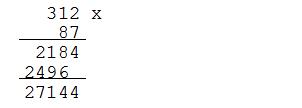
S-a luat deci fiecare cifra a inmultitorului si s-a efectuat produsul partial corespunzator, corectand la fiecare pas rezultatul prin calculul transportului. Rezultatul pentru fiecare produs partial s-a scris din ce in ce mai in stanga, pentru a se alinia corect ordinele de marime. Acest procedeu este oarecum incomod de implementat. Se pot face insa unele observatii care usureaza mult scrierea codului:

Prin inmultirea cifrei cu ordinul de marime 10i din primul numar cu cifra cu ordinul de marime 10j din al doilea numar se obtine o cifra corespunzatoare ordinului de marime 10i+j in rezultat (sau se obtine un numar cu mai mult de o singura cifra, caz in care transportul merge la cifra corespunzatoare ordinului de marime 10i + j + 1).
Daca numerele au M si respectiv N cifre, atunci produsul lor va avea fie M + N fie M + N - 1 cifre. Intr-adevar, daca numarul A are M cifre, atunci 10^M-1 ≤ A < 10^M si 10^N-1 ≤ B < 10^N, de unde rezulta 10^M+N-2 ≤ A x B < 10^M+N.
La calculul produselor partiale se poate omite calculul transportului, acesta urmand a se face la sfarsit. Cu alte cuvinte, intr-o prima faza putem pur si simplu sa inmultim cifra cu cifra si sa adunam toate produsele de aceeasi putere, obtinand un numar cu "cifre" mai mari ca 9, pe care il aducem la forma normala printr-o singura parcurgere. Sa reluam acelasi exemplu:

Aceasta operatie efectueaza MxN produse de cifre si M+N (sau M+N-1, dupa caz) "transporturi" pentru aflarea rezultatului, deci are complexitatea O(MxN). Iata si implementarea:

void MultHuge(Huge A, Huge B, Huge C)
/* C <- A x B */
{ int i,j,T=0;

  C[0]=A[0]+B[0]-1;
  for (i=1;i<=A[0]+B[0];) C[i++]=0;
  for (i=1;i<=A[0];i++)
    for (j=1;j<=B[0];j++)
      C[i+j-1]+=A[i]*B[j];
  for (i=1;i<=C[0];i++)
    { T=(C[i]+=T)/10;
      C[i]%=10;
    }
  if (T) C[++C[0]]=T;
}

Mai exista o alta modalitate de a inmulti doua numere de cate N cifre fiecare, care are complexitatea 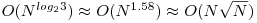$O(N^{log_2 3}) \approx O(N^{1.58}) \approx O(N \sqrt{N})$ . Ea deriva de un algoritm propus de Strassen in 1969 pentru inmultirea matricelor. Diferenta se face simtita, ce-i drept pentru valori mari ale lui N, dar constanta multiplicativa creste destul de mult si, in plus, solutia e mai greu de implementat; de aceea nu recomandam implementarea ei in timpul concursului. Ideea de baza este sa se micsoreze numarul de inmultiri si sa se mareasca numarul de adunari, deoarece adunarea a doi vectori se face in O(N), pe cand inmultirea se face in O(N 2). Sa consideram intregii A si B, fiecare de cate N cifre. Trebuie sa-i inmultim intr-un timp T(N) mai bun decat O(N 2). Sa impartim numarul A in doua "bucati" C si D, fiecare de cate N/2 cifre, iar intregul B in doua bucati E si F, tot de cate N/2 cifre (presupunem ca N este par):

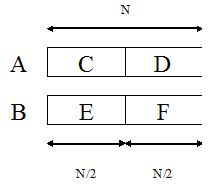
Atunci se poate scrie relatia:
A x B = (C x 10^N/2 + D) x (E x 10^N/2 + F) = CE x 10^N + (CF + DE) x 10^N/2 + DF

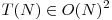Pentru a putea calcula produsul A x B avem, prin urmare, nevoie de patru produse partiale, de trei adunari si de doua inmultiri cu puteri ale lui 10. Adunarile si inmultirile cu puteri ale lui 10 se fac in timp liniar. Daca efectuam cele patru produse partiale prin patru inmultiri, rezulta formula recurenta de calcul T(N)=4T(N/2)+O(N) care duce prin eliminarea recurentei la $T(N)\in O(N)^2$ . Cu alte cuvinte, inca n-am castigat nimic. Trebuie sa reusim cumva sa reducem numarul de inmultiri de la 4 la 3, chiar daca prin aceasta vom mari numarul de adunari necesare. Sa definim produsul G = (C + D) x (E + F) = CE + CF + DE + DF = CE + DF + (CF + DE)
Atunci putem scrie: A x B = CE x 10^N + (G - CE - DF) x 10^N/2 + DF
Pentru aceasta varianta, folosim doar trei inmultiri, si chiar daca avem nevoie de sase adunari si scaderi si doua inmultiri cu puteri ale lui 10, complexitatea se va reduce la 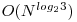$O(N^{log_2 3})$ . In cazul in care N este o putere a lui 2, impartirea in doua a numerelor se poate face fara probleme la fiecare pas, pana se ajunge la numere de o singura cifra, care se inmultesc direct. In cazul in care N nu este o putere a lui 2, este comod sa se completeze numerele cu zerouri pana la o putere a lui 2. In functiile descrise mai jos, MultRec nu face decat inmultirea recursiva, pe cand MultVect2 se ocupa si de corectarea numarului de cifre (incrementarea pana la o putere a lui 2). Pentru calculul produselor C x E si D x F, procedura MultRec se autoapeleaza; pentru calcularea produsului (C+D) x (E+F), insa, este nevoie sa fie apelata procedura MultVect2, deoarece prin cele doua adunari poate sa apara o crestere a numarului de cifre al factorilor, care in acest caz trebuie readusi la un numar de cifre egal cu o putere a lui 2.

void MultHuge2(Huge A, Huge B, Huge P);
void MultRec(Huge A, Huge B, Huge P)
{ Huge C,D,E,F,CE,DF;
  if (A[0]==1)
    { P[1]=A[1]*B[1];
      P[0]=(P[2]=P[1]/10)>0 ? 2 : 1;
      P[1]%=10;
    }
    else { P[0]=0;
           AtribHuge(C,A);Shr(C,A[0]/2);
           AtribHuge(D,A);D[0]=A[0]/2;
           AtribHuge(E,B);Shr(E,B[0]/2);
           AtribHuge(F,B);F[0]=B[0]/2;
           MultRec(C,E,CE);MultRec(D,F,DF);
           Add(C,D);Add(E,F);
           MultHuge2(C,E,P);
           Subtract(P,CE);Subtract(P,DF);
           Shl(P,A[0]/2);
           Shl(CE,A[0]);Add(P,CE);
           Add(P,DF);
         }
}
void MultHuge2(Huge A, Huge B, Huge P)
/* P <- A x B, varianta NA(lg 3) */
{ int i,j,NDig=A[0]>B[0] ? A[0] : B[0],Needed=1,SaveA,SaveB;
  /* Corecteaza numarul de cifre */
  while (Needed<NDig) Needed<<=1;
  SaveA=A[0];SaveB=B[0];A[0]=B[0]=Needed;
  for (i=SaveA+1;i<=Needed;) A[i++]=0;
  for (i=SaveB+1;i<=Needed;) B[i++]=0;
  MultRec(A,B,P);
  /* Restaureaza numarul de cifre */
  A[0]=SaveA;B[0]=SaveB;
  while (!P[P[0]] && P[0]>1) P[0]--;
}

Impartirea unui vector la un scalar

Ne propunem sa scriem o functie care sa imparta numarul A de tip Huge la scalarul B, sa retina valoarea catului tot in numarul A si sa intoarca restul (care este o variabila scalara). Sa pornim de la un exemplu particular si sa generalizam apoi procedeul: sa calculam catul si restul impartirii lui 1997 la 7. Cu alte cuvinte, sa gasim acele numere C de tip Huge si 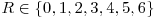$R\in\{0, 1, 2, 3, 4, 5, 6\}$ cu proprietatea ca 1997 = 7 x C + R.

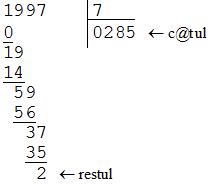
La fiecare pas se coboara cate o cifra de la deimpartit alaturi de numarul deja existent (care initial este 0), apoi rezultatul se imparte la impartitor (7 in cazul nostru). Catul este intotdeauna o cifra si se va depune la sfarsitul catului impartirii, iar restul va fi folosit pentru urmatoarea impartire. Restul care ramane dupa ultima impartire este tocmai R pe care il cautam. Procedeul functioneaza si atunci cand deimpartitul are mai multe cifre. La sfarsit trebuie sa decrementam corespunzator numarul de cifre al catului, prin neglijarea zerourilor create la inceputul numarului. Numarul maxim de cifre al catului este egal cu cel al deimpartitului.

unsigned long Divide(Huge A, unsigned long X)
/* A <- A/X si intoarce A%X */
{ int i;
  unsigned long R=0;

  for (i=A[0];i;i--)
    { A[i]=(R=10*R+A[i])/X;
      R%=X;
    }
  while (!A[A[0]] && A[0]>1) A[0]--;
  return R;
}

Daca dorim numai sa aflam restul impartirii, nu mai avem nevoie decat sa recalculam restul la fiecare pas, fara a mai modifica vectorul A:

unsigned long Mod(Huge A, unsigned long X)
/* Intoarce A%X */
{ int i;
  unsigned long R=0;

  for (i=A[0];i;i--)
    R=(10*R+A[i])%X;
  return R;
}

Impartirea a doi vectori

Daca se dau doi vectori A si B si se cere sa se afle catul C si restul R, etapele de parcurs sunt aceleasi ca la punctul precedent, numai ca operatorii "/" si "%" trebuie implementati de utilizator, ei nefiind definiti pentru vectori. Cu alte cuvinte, dupa ce "coboram" la fiecare pas urmatoarea cifra de la deimpartit, trebuie sa aflam cea mai mare cifra X astfel incat impartitorul sa se cuprinda de X ori in restul de la momentul respectiv. Acest lucru se face cel mai comod prin adunari repetate: pornim cu cifra X=0 si o incrementam, micsorand concomitent restul, pana cand restul care ramane este prea mic. Sa efectuam aceeasi impartire, 1997:7, considerand ca ambele numere sunt reprezentate pe tipul Huge.

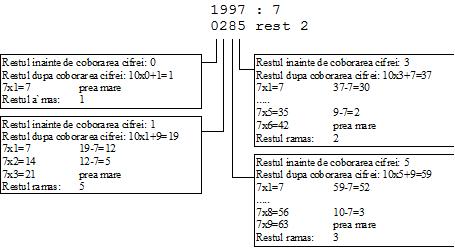
Cazul cel mai defavorabil (cand X=9) presupune 9 scaderi si 10 comparatii, cazul cel mai favorabil (cand X=0) presupune numai o comparatie, deci cazul mediu presupune 4 scaderi si 5 comparatii. Cautarea lui X se poate face si binar, prin injumatatirea intervalului, ceea ce reduce timpul mediu de cautare la aproximativ 3 comparatii si 3 inmultiri, dar codul se complica nejustificat de mult (de cele mai multe ori).

void DivideHuge(Huge A, Huge B, Huge C, Huge R)
/* A/B = C rest R */
{ int i;

  R[0]=0;C[0]=A[0];
  for (i=A[0];i;i--)
    { Shl(R,1);R[1]=A[i];
      C[i]=0;
      while (Sgn(B,R)!=1)
        { C[i]++;
          Subtract(R,B);
        }
    }
  while (!C[C[0]] && C[0]>1) C[0]--;
}

Extragerea radacinii cubice

Vom sari peste prezentarea algoritmului de extragere a radacinii patrate, pe care il vom lasa ca tema cititorului, si ne vom indrepta atentia asupra celui de extragere a radacinii cubice, care este putin mai complicat, dar care poate fi usor extins pentru radacini de orice ordin. Problema este exact cea din enunt, asa ca vom porni de la exemplul dat. Sa notam 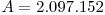$A = 2.097.152$ si $X = \sqrt[3]{A}$ . Cum se afla X ?

O prima varianta ar fi cautarea binara a radacinii, prin injumatatirea intervalului. Initial se porneste cu intervalul (1,A), deoarece radacina cubica se afla undeva intre 1 si A (evident, incadrarea este mai mult decat acoperitoare; ea ar putea fi mai limitativa, dar nu ar reduce timpul de lucru decat cu cateva iteratii). La fiecare pas, intervalul va fi injumatatit. Cum, probabil ca stiti deja; se ia jumatatea intervalului, se ridica la puterea a treia si se compara cu A. Daca este mai mare, inseamna ca radacina trebuie cautata in jumatatea inferioara a intervalului. Daca este mai mica, vom continua cautarea in jumatatea superioara a intervalului. Daca cele doua numere sunt egale, inseamna ca am gasit tocmai ce ne interesa. Prima varianta a pseudocodului este:

citeste A cu N cifre
  Lo <- 1, Hi <- A, X <- 0
  cat timp X=0
    Mid <- (Lo+Hi)/2
    daca Mid^3<A
      atunci Lo <- Mid+1
      altfel daca Mid^3>A
               atunci Hi <- Mid-1
               altfel X <- Mid

In cazul cel mai rau, algoritmul de mai sus efectueaza log ₂ A injumatatiri de interval, fiecare din ele presupunand o adunare, o impartire la 2 si o ridicare la cub. Dintre aceste operatii, cea mai costisitoare este ridicarea la cub, O( N² ). Complexitatea totala este prin urmare O( N² log ₂ A ). Deoarece A are ordinul de marime 10^N, rezulta complexitatea O( N³ log 10 )= O( N³ ), adica mai proasta decat cea ceruta (de altfel, un algoritm cu aceasta complexitate nici nu s-ar incadra in timp pentru N=1000). Daca timpul ne permite, trebuie sa cautam alta metoda.

In exemplul ales, sa observam ca 106≤A<109, de unde deducem ca 102≤X<103. Cu alte cuvinte, X are 3 cifre. In cazul general, daca A are N cifre, atunci X are [N/3] cifre (prin [N/3] se intelege "cel mai mic intreg mai mare sau egal cu N/3"). Care ar putea fi prima cifra a lui X? Daca X incepe cu cifra 2, atunci 200≤X<300 => 8.000.000≤2.097.152<27.000.000, ceea ce este fals. Cu atat mai putin poate prima cifra a lui X sa fie mai mare ca 2. Rezulta ca prima cifra a lui X este 1. De altfel, pentru a afla acest lucru, putem sa si neglijam ultimele 6 cifre ale lui A. Ne intereseaza doar prima cifra, cea a milioanelor, iar prima cifra a lui X o alegem in asa fel incat cubul ei sa fie mai mic sau egal cu 2.

Ce putem spune despre a doua cifra? Daca ar fi 3, atunci 130≤X<140 => 2.197.000≤2.097.152<2.744.000, fals (deci cifra este cel mult 2). Daca ar fi 1, atunci 110≤X<120 => 1.331.000≤2.097.152<1.728.000, fals. Rezulta ca a doua cifra este obligatoriu 2. Analog, putem neglija ultimele trei cifre ale lui A, iar a doua cifra a lui X este cel mai mare C pentru care $\overline{1C}^3 \leq 2097$ . Pentru a afla ultima cifra, aplicam acelasi rationament: Daca ar fi 9, atunci X=129 si ar rezulta 2146688=X³=2097152, absurd. Daca consideram ca cifra este 8, atunci calculul se verifica. Am aflat asadar ca X=128.

Procedeul general este urmatorul: dandu-se un numar A cu N cifre, il completam cu zerouri nesemnificative pana cand N se divide cu 3 (poate fi necesar sa adaugam maxim doua zerouri). Numarul de cifre semnificative ale radacinii cubice este M=N/3. Aflam pe rand fiecare cifra, incepand cu cea mai semnificativa. Sa presupunem ca am aflat cifrele X _M, X _M-1,..., X _K+1. Cifra X_K este cea mai mare cifra pentru care numarul 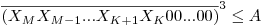$\overline{(X_MX_{M-1}...X_{K+1}X_K00...00)}^3\leq A$ . Cifra X_K este unica, deoarece exista, in general, mai multe cifre care verifica proprietatea ceruta, dar una singura este "cea mai mare". O a doua versiune a pseudocodului este deci:

citeste A cu N cifre
  X <- 0; T <- 0
  cat timp N%3<>0 adauga un 0 nesemnificativ
  repeta de N/3 ori
    adauga la T urmatoarele 3 cifre din A
    adauga la X cea mai mare cifra astfel incat X^3<= T

Sa evaluam complexitatea acestei versiuni. Linia 1 se executa in timp liniar, O(N). Liniile 2 si 3 se executa in timp constant. Linia 5 se executa in O(N), iar linia 6 presupune adaugarea unei cifre (O(N)) si o ridicare la cub, adica doua inmultiri (O(N²)). Deoarece liniile 5 si 6 se executa de N/3 ori (linia 4), rezulta o complexitate de O(N³). Iata ca nici acest algoritm nu a adus imbunatatiri si pare si ceva mai greu de implementat. El poate fi totusi modificat pentru a-i scadea complexitatea la O(N²).

Principalul neajuns al sau este efectuarea ridicarii la cub, care se face in O(N²). Daca am putea sa-l aflam la fiecare pas pe X³ fara a efectua inmultiri, adica in timp liniar, atunci intregul algoritm ar avea complexitate patratica. Bineinteles, prima intrebare care vine pe buzele cititorului este "cum sa ridicam la cub fara sa facem inmultiri?". Sa nu uitam insa ceva: ca noi nu-l cunoastem numai pe X. Il cunoastem si pe X de la pasul anterior, care avea o cifra mai putin (il vom boteza OldX). Sa presupunem ca, printr-o metoda oarecare, am reusit sa-l ridicam pe OldX la puterile a doua si a treia (si am obtinut numerele OldX2 si OldX3). Cum putem, cunoscand aceste trei numere, precum si noua cifra ce se va adauga la sfarsitul lui X (sa-i spunem C ), sa-l aflam pe X, patratul si cubul sau? Nu e prea greu:

$X = 10 \cdot OldX + C$
$X^2 = (10 \cdot OldX + C)^2 = 100 \cdot OldX^2 + 20 \cdot OldX \cdot C + C^2 = 100 \cdot OldX2 + (20 \cdot C) \cdot OldX + C^2$

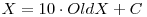
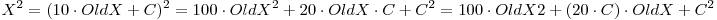
Iata asadar ca pentru a afla noile valori ale puterilor 1, 2 si 3 ale lui X, folosindu-le pe cele vechi, nu avem nevoie decat de adunari si de inmultiri cu numere mici (de ordinul miilor). Toate aceste operatii se fac in timp liniar, deci am reusit sa gasim un algoritm patratic. Iata mai jos sursa C:

void FindDigit(Huge L,Huge NewL2,Huge NewL3,
     Huge OldL,Huge OldL2,Huge OldL3,Huge Target)
{ Huge Aux;
  L[1]=10;
  do
    { L[1]--;
      /* Trebuie calculat LA3. Se stiu OldL (L/10)
         si noua cifra L[1]. Deci (OldL*10+L[1])A3=?
         Se aplica binomul lui Newton. */
      AtribHuge(NewL3,OldL3);Shl(NewL3,3);
      AtribHuge(Aux,OldL2);Mult(Aux,300*L[1]);
      Add(NewL3,Aux);
      AtribHuge(Aux,OldL);Mult(Aux,30*L[1]*L[1]);
      Add(NewL3,Aux);
      AtribValue(Aux,L[1]*L[1]*L[1]);
      Add(NewL3,Aux);
    }
  while (Sgn(NewL3,Target)==1);
  /* Aceeasi operatie pentru LA2 */
  AtribHuge(NewL2,OldL2);Shl(NewL2,2);
  AtribHuge(Aux,OldL);Mult(Aux,20*L[1]);
  Add(NewL2,Aux);
  AtribValue(Aux,L[1]*L[1]);
  Add(NewL2,Aux);
  /* Noile valori devin 'vechi' */
  AtribHuge(OldL2,NewL2);
  AtribHuge(OldL,L);
  AtribHuge(OldL3,NewL3);
}
void CubeRoot(Huge A, Huge X)
{ Huge Target,OldX,OldX2,OldX3,NewX2,NewX3;
  int i;
  /* Se initializeaza vectorii cu 0 (nici o cifra) */
  OldX[0]=OldX2[0]=OldX3[0]=X[0]=0;
  for (i=1;i<=(A[0]+2)/3;i++)
    { AtribHuge(Target,A);
      Shr(Target,3*((A[0]+2)/3-i));
      Shl(X,1);
      FindDigit(X,NewX2,NewX3,OldX,OldX2,OldX3,Target);
    }
}

Acum nu mai avem decat sa scriem rutinele de intrare/iesire si programul principal:

#include <stdio.h>
#include <mem.h>
#define NMax 1000
typedef int Huge[NMax+3];
Huge A,X; /* A[0] si X[0] indica numarul de cifre */

void ReadData(void)
{ FILE *F=fopen("input.txt","rt");
  int C,i;

  A[0]=0;
  do A[++A[0]]=(C=fgetc(F))-'0';
  while (C!=EOF);
  A[0]--;
  fclose(F);
  /* Intoarce vectorul pe dos */
  for (i=1;i<=A[0]/2;i++)
    A[i]=(A[i]AA[A[0]+1-i])A(A[A[0]+1-i]=A[i]);
}
void WriteSolution(void)
{ FILE *F=fopen("output.txt","wt");
  int i=X[0];
  while (!X[i]) i--;
  while (i) fputc(X[i--]+'0',F);
  fclose(F);
}
void main(void)
{
  ReadData();
  CubeRoot(A,X);
  WriteSolution();
}

Pentru a extinde aceasta metoda la radacini de orice ordin K, trebuie numai sa tinem cont de expresia binomului lui Newton:

$X^p = (10 \cdot OldX + C)^p = \sum_{\substack {0\leq i \leq p}} {10^i \cdot Oldx^i \cdot C^{p-i}}$

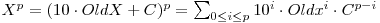
Presupunand ca avem calculate toate puterile de la 1 la p ale lui OldX, se poate calcula noua valoare a lui X^p folosind numai adunari si inmultiri cu scalari. In felul acesta se pot calcula in timp liniar valorile lui X, X², X³, ...., X^K.

Problema

Timp de implementare	Timp de rulare	Complexitate
1h 30'	10 secunde	O(N²)

Se da un numar natural cu N≤1000 cifre. Se cere sa se extraga radacina cubica a numarului. Se garanteaza ca numarul citit este cub perfect.
Fisierul INPUT.TXT contine un singur rand, terminat cu EOF, pe care se afla numarul, cifrele fiind nedespartite.
In fisierul OUTPUT.TXT se va tipari radacina cubica a numarului, pe o singura linie terminata cu EOF.

INPUT.TXT	OUTPUT.TXT
2097152	128

Rezolvare

Problema este cat se poate de simpla din punct de vedere matematic; dificultatea apare la implementare, atat datorita structurilor de date necesare, cat mai ales datorita complexitatii cerute. Despre lucrul cu numere intregi (chiar si Longint) nici nu poate fi vorba, iar la lucrul cu numere reale apar erori de calcul.

Structura de date propusa pentru abordarea acestui gen de probleme este urmatoarea: numerele vor fi reprezentate printr-un vector de cifre zecimale. Prima pozitie (pozitia 0) din vector este rezervata pentru a memora numarul de cifre. Definitia C a tipului de date este:

typedef int Huge[1001];

Iata cum s-ar memora numarul "1997" intr-un asemenea vector:

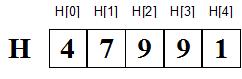
Se observa ca vectorul este oarecum "intors pe dos". Totusi, aceasta forma este cea mai convenabila, pentru ca ea permite implementarea cu o mai mare usurinta a operatiilor aritmetice.

Mai trebuie remarcat ca pe fiecare pozitie K in vector se afla cifra care il reprezinta pe 10^K-1 in numarul reprezentat: in V¹ se afla cifra unitatilor (10⁰), in V² se afla cifra zecilor (10¹), in V³ se afla cifra sutelor (10²) s.a.m.d. Formatul zecimal nu este cea mai fericita (a se citi "eficienta") alegere. El ocupa doar patru biti din cei opt ai unui octet, deci face risipa de memorie. Daca am alege baza de numeratie 256, am folosi la maximum memoria, si in plus operatiile ar fi cu mult mai rapide (deoarece 256 este o putere a lui 2, inmultirile si impartirile la 256 sunt simple deplasari la stanga si la dreapta ale reprezentarilor binare). Sa facem urmatorul calcul ca sa vedem cate cifre are in baza 256 un numar care are 1000 de cifre in baza 10:

$10^{1000} = 10 \cdot (10^3)^{333} \approx 10 \cdot (2^10)^{333} \approx 10 \cdot (2^8)^{335} = 10 \cdot 256^{335}$

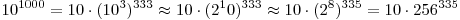
Asadar, numarul de cifre s-a redus cam de trei ori. Un algoritm liniar ar functiona de trei ori mai repede pe reprezentari in baza 256, iar unul patratic ar functiona de noua ori mai repede. Inconvenientul major este dificultatea depanarii unui program care opereaza intr-o baza aritmetica atat de straina noua. Vom ramane deci la baza 10, cu mentiunea ca acei mai temerari dintre voi pot incerca folosirea bazei 256.

infoarena informatica de performanta