Soluţia problemei Heist

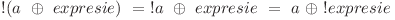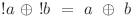Prima observaţie importantă este că $!(a\ \oplus\ expresie)\ = \ !a\ \oplus\ expresie\ = \ a\ \oplus\ !expresie$ si ca $!a\ \oplus\ !b\ =\ a\ \oplus\ b$ . Aşadar ne dăm seama că orice expresie poate fi rescrisă fără semne de negaţie sau cu un singur semn de negaţie, în funcţie de paritatea numărului semnelor de negaţie care apar în expresia iniţială.

Cum operaţia xor e asociativă şi comutativă şi 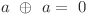$a\ \oplus\ a =\ 0\$ , putem scrie orice expresie fara paranteze si fiecare variabila sa apara fie o data, fie deloc. Astfel singurele expresii pe care trebuie sa le luam in considerare sunt cele cu maxim n variabile in care putem avea maxim un semn de negatie. In total sunt 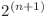$2^{(n+1)}$ astfel de expresii deci daca le-am genera pe toate si le-am evalua cu un backtracking, complexitatea finala ar fi 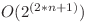$O(2^{(2*n+1)})$ , o solutie care daca este suficient de bine optimizata poate sa ia 60 de puncte.

Ne dam seama ca daca pe prima pozitie din sirul de biti apare 1, atunci semnul de negatie apare neaparat. La fel daca pe prima pozitie din sirul de biti apare 0, atunci nu avem semn de negatie. Astfel putem determina in 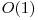$O(1)$ daca avem negatie sau nu. Daca avem negatie, putem nega intreg sirul de biti si putem rezolva problema la fel ca in cazul in care nu avem negatie.

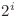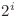Daca indexam sirul de biti de la 0, stim ca bitul de pe pozitia $2^i$ , unde $0 \le i \le n$ , ii corespunde valorii expresiei atunci cand toate variabilele mai putin variabila cu ordinul $(n\ -\ i)$ sunt egale cu 0. Daca bitul de pe pozitia $2^i$ are valoarea 0 inseamna ca variabila nu apare in expresie, iar daca are valoarea 1 inseamna ca variabila apare in expresie. Astfel am determinat in 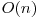$O(n)$ o expresie posibil valida. Trebuie sa verificam daca expresia determinata este corecta, asta fiind foarte usor cu un backtracking in 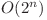$O(2^n)$ , o solutie de complexitate 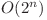$O(2^n)$ obtinand 100 de puncte.

infoarena informatica de performanta

Soluţia problemei Heist